1 Ответ
Задание 1: В волшебной лавке продаются волшебные кубики, шары и конусы. Все фигурки одного типа стоят одинаково, а разные — возможно, по-разному. Волшебник собрал несколько наборов и расположил их на витрине в порядке возрастания стоимости. Потом он собрал ещё один набор. Куда его следует положить на витрине, чтобы все наборы по-прежнему лежали по возрастанию стоимости?
Ответ на скрине:
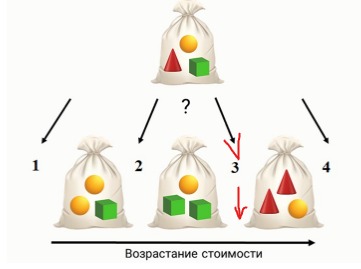
Пояснение:
Например:
1 шарик = 1 руб.
1 кубик = 2 руб.
1 конус = 3 руб.
Значит, в первом мешочке 4 рубля, во втором мешочке 5 рублей, в третьем мешочке 7 рублей. Тот мешочек, который собрал волшебник, будет равняется 6 рублей. Значит он должен стоять после 5 рублей. И так мы получим цепочку по возрастанию. 4 руб., 5руб.,6 руб., 7 руб.
Задание 2: Петя играет в игру: на экране есть клетчатый квадрат размером 4×4.Каждая клетка окрашена либо в чёрный, либо в белый цвет. За один ход можно поменять местами либо два столбца, либо две строки. Например, из раскрашенного в шахматном порядке квадрата можно за один ход получить такие квадраты, как на рисунке. В этот раз у Пети на экране квадрат, раскрашенный, как показано на рисунке 2. Какие квадраты сможет получить Петя за один или несколько ходов? = 2, 4
Задание 3: Кирилл сложил из нескольких одинаковых красных кубиков куб побольше. Например, на рисунке из кубиков выложен куб со стороной в 2 кубика. Затем Кирилл взял точно такие же по размеру маленькие зелёные кубики и обложил ими в один слой весь красный куб так, что получился куб, зелёный снаружи. Сколько для этого ему понадобилось зелёных кубиков, если красный куб выложен из 125 маленьких?
Решение:
Если красный куб сложен из 125 маленьких одинаковых кубиков, значит, длина стороны этого большого куба равна корню кубическому из 125, то есть 5 кубиков.
При обложении зелёными кубиками в один слой, сторона куба увеличится на 2 (по одному кубику с каждого края). Значит, новый куб будет иметь сторону равную 5 + 2 = 7 кубикам.
Объем большого куба можно найти, возведя длину его стороны в куб: 7^3 = 343 кубика.
Ответ: Кириллу понадобилось 343 зелёных кубика — 125 красных кубиков = 218 зелёных кубиков.
Задание 4: Филя нашёл старую таблицу расстояний (по дорогам) между сёлами, но названия всех сёл, кроме Ох, оказались стёрты. Филя нарисовал схематическую (то есть если на рисунке одна дорога длиннее другой, то на самом деле может быть не так) карту дорог. Установите соответствие между названиями сёл и их номерами, пользуясь таблицей. Если клетка пуста, это значит, что прямой дороги между сёлами нет.
Ответ: Ах — 1, Ух — 4, Их — 2, Эх — 3, Юх — 5
Задание 5: В одной семье детей зовут Саша, Женя и Валя. Все они родились в один день, но в три разных года. Известно, что Саша старше своего брата на 10 лет, а возраст одной из девочек равен сумме возрастов её брата и сестры. Также известно, что сумма возрастов всех детей равна 40 годам, а Женя не младше всех.
Как зовут мальчика? Впишите только имя. - Валя
Сколько лет Саше? Впишите только число! - 15
Сколько лет Жене? Впишите только число! — 20
Сколько лет Вале? Впишите только число! — 5
Задание 6: В автомате продаются шоколадки трёх видов — А, Б и В. Макс хочет купить несколько шоколадок, чтобы из некоторых из них (не ломая) сложить квадрат 3×3. Он видит, что в автомате лежит 1 шоколадка вида А, 3 — вида Б и 7 — вида В. Шоколадки выдаются случайным образом, выбрать конкретные нельзя.
Какую минимальную сумму стоит приготовить Максу, чтобы наверняка справиться с задачей, если одна шоколадка стоит 100 руб.? Ответ выразите в рублях.

Решение:
Если бы Макс мог выбрать шоколадку, тогда ему потребовалось бы всего 300 рублей, чтобы собрать квадрат 3×3. Но так как выбор разный, тогда получаем: 100 (А) + 300 (Б) + 100 (В) = 500 рублей. Ну или ему повезет и он вытянет сразу нужные шоколадки.
Задание 7: У Васиного дедушки на стене висят четверо часов. Вася знает, что ни одни из них не показывают точное время: какие-то спешат на полчаса, а какие-то отстают на два часа. А ещё двое тоже врут, но как именно, Вася не помнит. Однажды Вася пришёл в гости к дедушке и увидел, что часы показывают время так, как изображено на рисунке.
Во сколько Вася пришёл к дедушке? Ответ запишите в формате ЧЧ:ММ. = 08:40
Задание 8: В группе из 10 рыцарей и лжецов все разного роста. Каждый заявил: «Среди нас найдутся 2 лжеца выше меня и 2 лжеца ниже меня».
Сколько среди этих 10 человек может быть лжецов? Укажите все варианты.
Решение:
Прежде всего, нужно понимать, что рыцари всегда говорят правду, а лжецы всегда лгут. По условию задачи, каждый из 10 человек заявляет, что среди них найдутся два лжеца, которые выше его, и два лжеца, которые ниже его.
Это значит, что ни самый высокий, ни самый низкий, ни второй по высоте, ни второй по низости не могут быть лжецами, так как их утверждение будет ложным. Это оставляет нам только четыре возможных лжецов.
Принимая во внимание, что лжецы лгут, каждый из этих четырех человек должен быть лжецом, чтобы его утверждение было ложным. Это даёт один возможный ответ:
Ответ: Всего может быть 4 лжеца.
