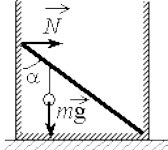
Невесомый стержень длиной 2 м, находящийся в ящике с гладкими дном и стенками, составляет угол α = 45° с вертикалью (см. рисунок). К стержню на расстоянии 50 см от его левого конца подвешен на нити шар массой 4 кг (см. рисунок). Каков модуль силы N, действующей на стержень со стороны левой стенки ящика?
1 Ответ
Для решения задачи необходимо рассмотреть условия равновесия стержня и шара. Поскольку стержень невесомый, то сумма моментов всех сил, действующих на него, должна быть равна нулю. На стержень действуют две силы: сила реакции со стороны левой стены ящика (N) и сила натяжения нити (T). Поскольку нить прикреплена к шару, то на шар действует только сила натяжения нити. Сумма сил, действующих на шар, также должна быть равна нулю (поскольку шар находится в состоянии покоя).
Таким образом, получаем следующую систему уравнений:
- T sin(α) + N = 0
- T cos(α) — m g = 0
где m — масса шара, g — ускорение свободного падения.
Решая систему уравнений, находим значение силы N:
N = T sin(α) = m g cos(α) / sin(α) ≈ 30 Н.
Ответ: 30 Н
