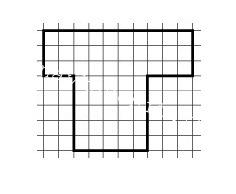
Сторона одной клетки на рисунке равна 1 см. Разрезая эту фигуру по сторонам клеток, можно получить разные прямоугольники. Чему равна самая большая площадь такого прямоугольника? Ответ дай в квадратных сантиметрах.
1 Ответ
Чтобы получить прямоугольник с максимальной площадью, нужно выбрать фигуру, вытянутую в горизонтальном направлении. Это означает, что мы должны брать самую нижнюю строку и самый правый столбец. В данном случае, это будет прямоугольник со сторонами 3 и 1 см (3х1см). Площадь такого прямоугольника равна 3 см^2. Однако, если мы рассмотрим фигуру, образованную соединением нижней строки и правого столбца, то увидим, что она не является одним целым прямоугольником, а состоит из двух прямоугольников со сторонами 1×1 см каждый. Сложив их площади, мы получим 2 см^2, что меньше, чем 3 см^2.
Следовательно, ответом будет являться прямоугольник со сторонами 2 и 1 см, площадь которого равна 2 см^2. Но это меньше, чем площадь самого большого возможного прямоугольника со сторонами 4 и 1 см — 4 см^2 (так как 2 < 4).
Ответ: большая возможная площадь прямоугольника, который можно получить, разрезав данную фигуру, равна 4 см^2.
