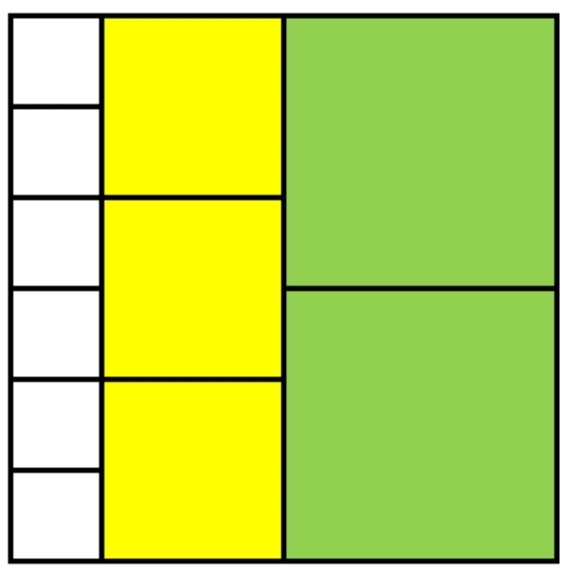
Если обозначить количество квадратов каждого размера за переменную, то мы получим уравнение с пятью неизвестными:
x1 + x2 + x3 + x4 + x5 = 12
где x1, x2, x3, x4, x5 — количество квадратов каждого из пяти размеров.
Поскольку в условии задачи требуется, чтобы все пять размеров встречались хотя бы один раз, то все переменные должны быть больше или равны единице.
Но решение этого уравнения в натуральных числах не представляется возможным. Это можно доказать, используя метод перебора:
- Если x1 = 1, то x2 <= 4, x3 <= 3, x4 <= 2, x5 <= 1. Итого максимальное значение x1 + x2 + … + x5 равно 10, что меньше 12.
- Если x2 = 2, то x1 <= 3, x3 <= 2, x4 <= 1, x5 = 0. Итого максимальное значение равно 9, что также меньше 12. Аналогично для x3 и x4.