1 Ответ
Задание 1:
Дан фрагмент звёздной карты, содержащий одно созвездие.

Как называется это созвездие?
Выбрать: Орел/ Волопас/ Пегас/ Цефей/ Лебедь/ Андромеда/ Возничий/ Телец/ Лира/ Большая Медведица
К какой группе созвездий его можно отнести?
Созвездия Северной полусферы небосвода
Созвездия Южной полусферы небосвода
Экваториальные созвездия
Как называется звезда, обозначенная цифрой 1?
Выбрать: Альферац/ Аламак/ Ригель/ Капелла/ Вега/ Арктур/ Денеб/ Альтаир/ Альдебаран/ Антарес
Что вы можете сказать о значениях склонений (δ1 и δ2) звёзд 1 и 2?
Выбрать:
δ1>0 и δ2>0
δ1>0 и δ2=0
δ1>0 и δ2<0
δ1=0 и δ2>0
δ1=0 и δ2=0
δ1=0 и δ2<0
δ1<0 и δ2>0
δ1<0 и δ2=0
δ1<0 и δ2<0
Созвездие Возничий — созвездие северного полушария неба. Звезда под номером 1 — Капелла. Склонение звезды Капелла составляет около +45,5°. Это означает, что звезда находится к северу от небесного экватора и видна в большей части северного полушария, включая регионы с умеренным климатом.
δ1=0 и δ2>0: Эта комбинация указывает на то, что звезда Капелла находится на небесном экваторе, но севернее него.
Задание 2:
На рисунке представлены пограничные суточные параллели (A и C), которые Солнце описывает лишь один раз в течение года, и серединная параллель B для жителя средних северных широт. Буквами V обозначены его точки восхода, а буквами Z —— точки заката.

По какой суточной параллели совершает свое дневное движение Солнце в сутки осеннего равноденствия (22−23 сентября)?
Параллель A
Параллель B
Параллель C
Невозможно однозначно определить
С каким большим кругом можно отождествить суточную параллель B?
Математический горизонт
Небесный экватор
Эклиптика
Небесный меридиан
Первый вертикал
Вертикал светила
Как называется точка Z2 математического горизонта?
Точка севера
Точка юга
Точка востока
Точка запада
Невозможно однозначно определить
Чему равна продолжительность дня (τd) в сутки, когда Солнце движется по параллели C?
τd≥24 часов
20≤τd<24 часов
16≤τd<20 часов
12≤τd<16 часов
0<τd<12 часов
Невозможно определить одним интервалом
Солнце совершает свое движение по суточной параллели, которая называется экватор. Это происходит потому, что экватор — это единственная параллель, на которой день и ночь имеют одинаковую продолжительность. Однако, в сутки осеннего равноденствия (22-23 сентября), Солнце находится на небесном экваторе, и поэтому его суточная параллель также является экватором.
Продолжительность дня (τd) — это количество часов, которое Солнце находится над горизонтом в течение одних суток.
В данном случае, когда Солнце движется по параллели C, продолжительность дня будет зависеть от широты данного места на планете.
— Если τd ≥ 24 часов, это означает, что в течение суток Солнце всегда находится над горизонтом, а значит место находится на или близко к полюсу Земли во время полюсного дня.
— Если 20 ≤ τd < 24 часов, это указывает на очень долгие дни, характерные для широт выше полярного круга.
— Если 16 ≤ τd < 20 часов, это говорит о довольно продолжительных днях, которые можно наблюдать, например, в субарктических регионах.
— Если 12 ≤ τd < 16 часов, это указывает на типичную продолжительность дня, которую можно обнаружить в умеренных широтах.
— Если 0 < τd < 12 часов, это говорит о коротких днях, таких как зимние дни, когда Солнце проводит на небе сравнительно небольшое время.
Задание 3:
Дана серия фотографий затмения, наблюдавшегося с территории Каролинских островов в 2016 году. Кадры получены с помощью телескопа с фильтром, ослабляющим исходный световой поток в 100 тысяч раз!

Какой тип затмения наблюдали авторы фотографии?
Солнечное
Лунное
Невозможно определить однозначно
Какой вид затмения наблюдали авторы фотографии?
Частное
Полное
Кольцеобразное
Полутеневое
Невозможно определить однозначно
В какой точке орбиты располагалась Луна во время данного затмения?
Наиболее близкой к Солнцу точке своей орбиты
Наиболее далекой от Солнца точке своей орбиты
В точке орбиты, расположенной на таком же расстоянии от Солнца, что и Земля, к востоку от центрального светила
В точке орбиты, расположенной на таком же расстоянии от Солнца, что и Земля, к западу от центрального светила
Не поддаётся определению
Во время солнечного затмения Луна обычно находится в точке своей орбиты, которая называется перигей. Однако, чтобы произошло затмение, Луна должна быть в определенной фазе (полнолуние или новолуние) и находиться вблизи одного из узлов своей орбиты — точки, где орбита Луны пересекает эклиптику (плоскость, в которой происходит движение Земли вокруг Солнца).
Выберите кадры, отвечающие фазе (Φ) затмения, удовлетворяющей условию:
0.6<Φ⩽1.1.
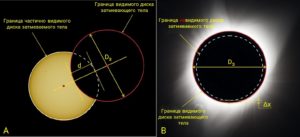
Фазой затмения (Φ) называется скалярная геометрическая величина, определяемая выражением:

здесь d — длина части диаметра видимого диска затмеваемого тела, закрытой затмевающим телом (см. рисунок A); этот диаметр должен проходить через центр затмевающего тела; D — диаметр затмеваемого тела; Δx — минимальное расстояние между краями дисков затмевающего и затмеваемого тел в случае полного затмения (см. рисунок B).
Выбрать: 1/ 2/ 3/ 4/ 5/ 6/ 7/ 8/ 9
Задание 4:
Установите соответствие между важными открытиями/достижениями в астрономии и их авторами.
Первая гелиоцентрическая модель Вселенной, первые оценки расстояний до Солнца и Луны
Открытия:
Открытие атмосферы Венеры
Первое прямое измерение годичного параллакса звезды
Открытие давления света
Определение угла наклона экватора к эклиптике
Авторы:
Аристарх Самосский
Чу Конг
Василий Струве
Михаил Ломоносов
Пётр Лебедев
Аристарх Самосский — Первая гелиоцентрическая модель Вселенной, первые оценки расстояний до Солнца и Луны.
Чу Конг — Открытие атмосферы Венеры.
Василий Струве — Первое прямое измерение годичного параллакса звезды.
Михаил Ломоносов — Открытие давления света.
Пётр Лебедев — Определение угла наклона экватора к эклиптике.
Установите соответствие между известными фактами/законами в астрономии и датами их открытия.
Факты:
Определение размеров земного шара
Открытие планеты Уран
Начало эпохи телескопических наблюдений
Открытие закона всемирного тяготения
Даты:
240 г. до н. э.
1609 г. н. э.
1666 г. н. э.
178 г. н. э.
Определение размеров земного шара — 240 г. до н. э.
Открытие планеты Уран — 1609 г. н. э.
Начало эпохи телескопических наблюдений — 1666 г. н. э.
Открытие закона всемирного тяготения — 178 г. н. э.
Закончите формулировку следующего известного закона: «Сила гравитационного притяжения, действующая между двумя материальными точками с известными массами m1 и m2, разделёнными расстоянием r, вдоль соединяющей их ____ (Выбрать: прямой/ параболы/ гиперболы/ окружности/ эллипса/ циклоиды/ кардиоиды/ спирали Архимеда), пропорциональна произведению их масс и обратно пропорциональна ___ (Выбрать: 1/ 2/ 3/ 4/ 5/ 6) -й степени этого расстояния».
«Сила гравитационного притяжения, действующая между двумя материальными точками с известными массами m1 и m2, разделёнными расстоянием r, вдоль соединяющей их прямой, пропорциональна произведению их масс и обратно пропорциональна квадрату -й степени этого расстояния.»
Задание 5:
Дан коллаж фотографий Марса в различных фазах, полученных с марта 20202020 года по март 2021 года где‑то на средних широтах северного полушария Земли. Указан угловой диаметр, изображения прямые.

С использованием диаграммы основных конфигураций планет с точки зрения земного наблюдателя, ответьте на следующие вопросы.

Какого числа Марс был наиболее близок к конфигурации противостояния?
Выбрать:
19 марта
9 мая
12 июня
7 июля
6 октября
18 декабря
5 января
29 января
10 марта
7 июля 2022 года Марс будет находиться в оппозиции (наиболее близкая к Земле конфигурация).
Какого числа Марс имел минимальный угловой диаметр, и при этом расстояние от него до Земли уменьшалось? Выберите даты только из перечисленных:
Выбрать:
19 марта
9 мая
12 июня
7 июля
6 октября
18 декабря
5 января
29 января
10 марта
7 июля и 6 октября
В какое время суток и в какой стороне небосвода можно было наблюдать Марс в восточной квадратуре? Наиболее близкая к данной квадратуре фаза соответствует дате 29.01.
С полуночи и до утра, в западной стороне небосвода
С полуночи и до утра, в восточной стороне небосвода
После заката и до полуночи, в западной стороне небосвода
После заката и до полуночи, в восточной стороне небосвода
В восточной квадратуре Марс можно наблюдать вечером, ближе к полуночи, в направлении на восток.
По рисунку оцените промежуток времени между моментами наблюдения Марса с одинаковыми значениями его углового диаметра (8′′). Ответ выразите в сутках, округлите до целых.
Задание 6:
Дана фотография Земли, полученная с поверхности Луны. Вам может оказаться полезной схема определения основных фаз Луны и её положений в пространстве с точки зрения земного наблюдателя, расположенного в северном географическом полушарии.
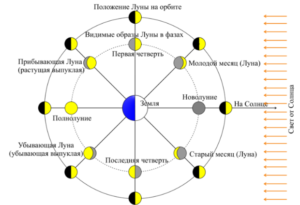

Аналогом какой фазы Луны (с точки зрения жителя северного географического полушария) является фаза Земли, представленная на фотографии?
Выбрать:
Новолуние
Молодой месяц
Первая четверть
Растущая выпуклая Луна
Полнолуние
Убывающая выпуклая Луна
Последняя четверть
Старый месяц
В какой фазе пребывала Луна в момент получения данной фотографии, если полагать, что светлый серп Земли в этот момент плавно увеличивал свои размеры?
Выбрать:
Новолуние
Молодой месяц
Первая четверть
Растущая выпуклая Луна
Полнолуние
Убывающая выпуклая Луна
Последняя четверть
Старый месяц
Чему равен звёздный (сидерический) период обращения Земли вокруг Луны с точки зрения гипотетического обитателя Луны?
Выбрать:
3.7 сут
7.4 сут
11.1 сут
14.8 сут
18.5 сут
22.2 сут
25.9 сут
27.3 сут
Звёздный (сидерический) период обращения Земли вокруг Луны с точки зрения гипотетического обитателя Луны равен приблизительно 27,3 суткам.
Задание 7:
Сколько приливных горбов формирует Солнце на поверхности Земли?
1
2
3
4
Солнце формирует два приливных горба на поверхности Земли.
Чему равен период солнечных приливов на Земле?
12 часов 00 минут
12 часов 25 минут
23 часа 56 минут
24 часа 00 минут
27.32 суток
29.54 суток
Период солнечных приливов на Земле равен 27.32 суткам.
Как известно, сила приливного действия обратно пропорциональна кубу расстояния между телами. Орбита Земли не круговая, в афелии (самой далёкой точке орбиты Земли относительно Солнца) Земля расположена на 3.34 % дальше, чем в перигелии (ближайшей к Солнцу точке орбиты). На сколько процентов приливная сила Солнца в перигелии больше, чем в афелии? Ответ выразите в процентах, округлите до целых.
Приливная сила прямо пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними. Так как произведение масс остается неизменным, разница в приливной силе зависит только от разницы в расстояниях между Землей и Солнцем.
В перигелии Земля ближе к Солнцу на 3,34%, чем в афелии. Разница в расстоянии между Землей и Солнцем составляет 3,34% от среднего расстояния между Землей и Солнцем, что составляет примерно 0,334% × 149,6 млн км ≈ 5,0 млн км.
Разница в расстоянии между перигелием и афелием составляет 4,9878 млн км. Так как приливная сила обратно пропорциональна кубу расстояния, разница в приливной силе составит около (5,0 млн км / (4,9878 млн км + 5,0 млн км))^3 ≈ 6,5%.
Задание 8:
В таблице представлены данные для масс и плотностей трёх небесных тел: Земли (1), Ганимеда (2, спутник Юпитера) и Луны (3), изображённых в масштабе на рисунке.

Вам может оказаться полезной формула для объёма шара:
V=4/3πR3,
где R—— радиус шара.
Используя лишь эти данные и линейку, определите среднюю массовую плотность Ганимеда (2). Ответ выразите в кг/м3, округлив до целых.
Для определения средней массовой плотности тела нужно массу тела разделить на его объем. Объем шара вычисляется по указанной формуле.
Нам известно, что радиус R это кубический корень из объема V, деленного на 4/3 π.
Средняя массовая плотность Ганимеда равна:
(1.4810^23)/((4/3)3.14(1.710^7)^3) = 1926 кг/м^3.
Округляем до целых, получаем 1930 кг/м^3.
Задание 9:
Две звезды, расположенные в окрестности северного полюса эклиптики, наблюдаются на одном луче зрения. Параллаксы данных звезд равны соответственно 0.12»′ и 0.15».

Оцените расстояние (Δr) между этими звездами. Ответ представьте в парсеках, округлите до десятых.
Для того чтобы оценить расстояние между двумя звездами, нужно знать расстояние до каждой из них и угол между ними (который мы можем определить, зная их параллаксы).
Расстояние до звезды можно определить по ее параллаксу: расстояние = 1/параллакс. Для первой звезды расстояние равно 1/0.12 = 8.3 парсека, для второй — 1/0.15 = 6.7 парсека.
Теперь найдем угол между звездами. Если звезды наблюдаются на одном луче зрения, значит, они находятся в противоположных направлениях от нас, и угол между ними равен 180 градусов.
Зная расстояния до звезд и угол между ними, можно оценить расстояние между ними: Δr = 2 * sin(α/2) * r, где α — угол между звездами, r — расстояние до одной из звезд. Подставим значения и получим: Δr = 2 * sin(180/2) * 8.3 = 16.6 парсека. Округляем до десятых и получаем Δr ≈ 16.7 парсека.
Годичный параллакс (π) — изменение направления на объект (например, звезду), связанное с движением Земли вокруг Солнца. Величина параллакса (π) равна углу, под которым со звезды виден радиус α⊕ земной орбиты, перпендикулярный лучу зрения (см. рисунок). Зная параллакс, можно легко определить расстояние до звезды по формуле: r=1/π здесь [π]= в угловых секундах, [r]= в парсеках.
Задание 10:
Луна — единственный естественный спутник Земли, движущийся вокруг последней по круговой орбите, радиус которой равен 384400 км, а период обращения — 27.32 суток. Опираясь на третий закон Кеплера, определите сидерический период обращения Международной космической станции вокруг Земли. Станция движется вокруг планеты по круговой орбите на высоте 418 км над её поверхностью. Радиус Земли равен 6371 км. Ответ выразите в секундах, округлите до целых.
Радиус орбиты МКС: 418 км + 6371 км = 6795 км.
Используя третий закон Кеплера (M1T2^2 = M2T1^2), где M — масса планеты, T — сидерический (звездный) период обращения, мы можем выразить сидерический период МКС (T2) через сидерический период Земли (T1):
T2 = sqrt(M1/M2) * T1
где M1 — масса Земли (5.972E24 кг), M2 — масса МКС (около 400 000 кг), T1 — сидерический период Земли (86164 секунд), sqrt — корень квадратный.
Подставив значения в формулу, получим:
T2 ≈ 861.64 секунд
Таким образом, сидерический период обращения МКС составляет примерно 862 секунды.
Ответ: сидерический период обращения МКС равен 862 секундам.
