Рассмотрим координатную плоскость, которую планируется очищать с использованием робота пылесоса. Робот-пылесос представляет собой квадрат размером k ×k со сторонами, параллельными осям координат. Изначально левый нижний угол робота находится в точке (0, 0), а правый верхний,
соответственно — в точке (k, k).
Вам дана последовательность из n перемещений робота по плоскости, i-е перемещение характеризуется направлением di, принимающим значения ‘N’ (вверх, увеличение координаты Y), ‘S’ (вниз, уменьшение координаты Y), ‘W’ (влево, уменьшение координаты X) или ‘E’ (вправо, увеличение координаты X), и целым числом ai — расстоянием, на которое робот перемещается.
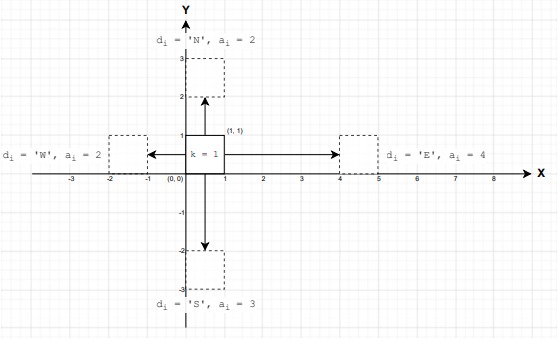
Робот в каждый момент времени убирает всю площадь под собой. Иными словами, точка считается убранной тогда и только тогда, когда она в какой-то момент времени принадлежала квадрату размера k × k, на котором находился робот. По заданным перемещениям робота посчитайте суммарную площадь всей убранной поверхности.
Формат входных данных
В первой строке ввода через пробел даны два целых числа: размер робота k и количество команд
n (1 <= k <+ 10^4; 1 <= n <= 10^5).
В i-й из следующих n строк через пробел даны направление i-го перемещения di и его расстояние
ai (di — буква ‘N’, ‘S’, ‘W’ или ‘E’; 1 <= ai <= 10^9).
Формат выходных данных
Выведите суммарную площадь убранной роботом поверхности.
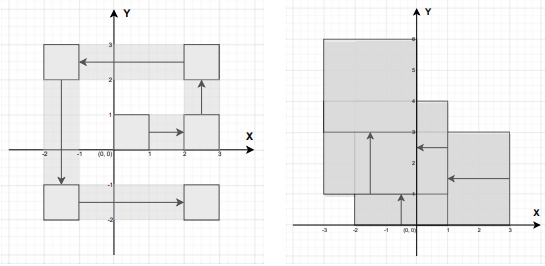
Ниже приведены иллюстрации к перемещениям робота согласно примерам из условия. Клетки,
которые робот посетил за время своих перемещений, затемнены.
1 Ответ
Полное решение заключается в объединении прямоугольников на плоскости. Это достаточно
классическая задача, которая имеет много аналогичных решений с использованием сканирующей
прямой и дерева отрезков. Одно из решений: будем хранить в дереве отрезков для каждой Y -координаты, сколько прямоугольников ее покрывают, и возвращать количество Y -координат, покрытых хотя бы одним прямоугольником. Альтернативный подход: используем дерево отрезков на минимум и суммарный вес минимумов, тогда если минимум равен 0, то это означает, что полоса не покрыта прямоугольниками. Так можно посчитать суммарную непокрытую площадь в некотором достаточно большом объемлющем прямоугольнике, а далее вычесть ее из его площади. Решение с деревом отрезков и сканирующей прямой работает за O(n log n).
Отметим в заключение, что координаты, в которых может оказываться робот, могут достигать 10^5·10^9 = 10^14, но площадь каждого посещенного прямоугольника не больше 10^4·10^9 = 10^13, а значит их общая площадь не превышает 10^5·10^4·109 = 10^18 и помещается в 64-битном типе данных.
Однако следует с осторожностью относится к промежуточным значениям, чтобы не произошло переполнения 64-битного типа данных.
