1 Ответ
Юрий Борисович начал строить на дачном участке теплицу (рис. 1). Для этого он сделал прямоугольный фундамент длиной 6 м (DС на рис. 2) и шириной 2,4 м (AD на рис. 2). Нижний ярус теплицы имеет форму прямоугольного параллелепипеда, собран из металлического профиля и по длине для прочности укреплён металлическими стойками. Высота нижнего яруса теплицы в два раза меньше её ширины. Для верхнего яруса теплицы Юрий Борисевич заказал металлические дуги в форме полуокружностей, которые крепятся к стойкам нижнего яруса. Отдельно требуется купить материал для обтяжки поверхности теплицы. В передней стенке планируется вход, показанный на рис. 1 прямоугольником EFKN, где точки Е, Р и N делят отрезок AD на равные части. Внутри теплицы Юрий Борисович планирует сделать три грядки: одну широкую центральную и две одинаковые узкие не краям, как показано на рис. 2. Между грядками и при входе в теплицу будут дорожки шириной 40 см, для которых надо купить тротуарную плитку размером 20 х 20 см.
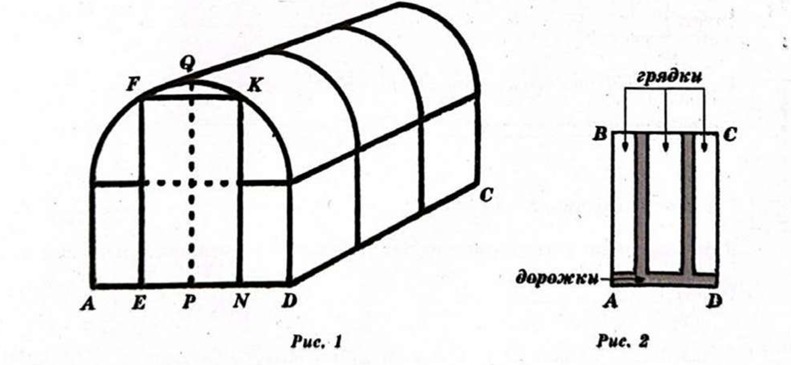
1. Найдите высоту теплицы PQ в метрах.
Ответ: 2,4
2. Сколько нужно купить упаковок плитки для дорожек, если в каждой упаковке 6 штук?
Ответ: 23
3. Найдите ширину центральной грядки, если она в 1,2 раза больше ширины узкой грядки.
Ответ: 60
4. Найдите длину металлической дуги для верхнего яруса теплицы. Ответ дайте в метрах, округлив его в большую сторону с точностью до десятых
Ответ: 3,8
5. Найдите высоту EF входа в теплицу в сантиметрах с точностью до целого
Ответ: 222, 223, 224, 225
6. Найдите значение выражения 45 + 0,6 · (–10)².
Ответ: 105
7. Какому из данных промежутков принадлежит число 5/13?
4) [0,5; 0,6]
1) [0,2; 0,3]
2) [0,3; 0,4]
3) [0,4; 0,5]
Ответ: 2
8. Найдите значение выражения √(17 · 5⁴) · √(17 · 2²)
Ответ: 850
9. Решите уравнение 2x² – 1 7/25 = 0. Если уравнение имеет больше одного корня, в ответ запишите меньший из корней.
Ответ: -0,8
10. У бабушки 25 чашек: 7 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Ответ: 0,72
11. Установите соответствие между графиками функций и формулами, которые их задают.
Ответ: 321
12. Площадь четырёхугольника можно вычислить по формуле s= 451а, где d1 did2 sin a и d2 — длины диагоналей четырёхугольника, а — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d1, если d2 =16, sina = 0,4, a S= 12,8.
Ответ: 4
13. Укажите решение неравенства 25x² ≥ 4.
Ответ: 2
14. В амфитеатре 24 ряда, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В пятом ряду 27 мест, а в седьмом ряду 31 место. Сколько мест в последнем ряду амфитеатра?
Ответ: 65
15. В треугольнике ABC известно, что AB = 14, BC = 5, sin∠ABC = 6/7. Найдите площадь треугольника ABC.
Ответ: 30
16. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK = 18, DK = 9, BC = 16. Найдите AD
Ответ: 8
17. В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
Ответ: 8
18. На клетчатой бумаге с размером клетки 1 × 1 отмечены три точки: A, B и C. Найдите расстояние от точки A до отрезка BC.
Ответ: 5
19. Какое из следующих утверждений верно? Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. Точка пересечения двух окружностей равноудалена от центров этих окружностей. Диагонали ромба точкой пересечения делятся пополам. В ответе запишите номер выбранного утверждения.
Ответ: 3
20. Решите уравнение (x – 3)⁴ – 3(x – 3)² – 10 = 0.
Ответ: 3-5; 3+5
21. Первый велосипедист выехал из посёлка по шоссе со скоростью 12 км/ч. Через час после него со скоростью 10 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа после этого догнал первого.
Ответ: 20 км\ч
22. Постройте график функции y = ((0,75x² – 1,5x) · |x|) / (x – 2). Определите, при каких значениях m прямая y = m не имеет с графиком ни одной общей точки.
Ответ: m=3
23. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 3,6, а AB = 8.
Ответ: 10
24. На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.

Ответ: доказано
25. В треугольнике ABC известны длины сторон AB = 36, AC = 54, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Ответ: 30
