1 Ответ
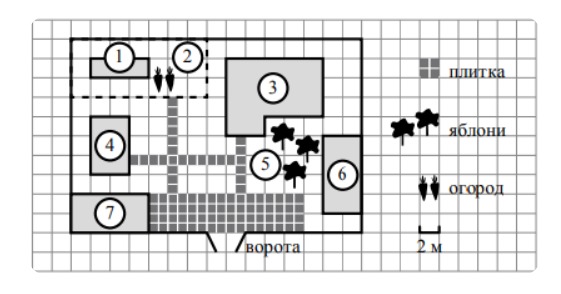
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.
Объекты яблони
теплицы
жилой дом
баня
Ответ: 5136
2. Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки?
Ответ: 6
3. Найдите площадь открытого грунта огорода (вне теплицы). Ответ дайте в квадратных метрах.
Ответ: 72
4. Найдите расстояние от ворот до сарая (расстояние между двумя ближайшими точками по прямой) в метрах.
Ответ: 10
5. Хозяин участка планирует установить в жилом доме систему отопления.
Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.
Нагреватель (котел) Прочее оборудование и монтаж Сред. расход газа / сред. потребл. мощность Стоимость газа / электро-энергии
Газовое отопление 22 000 руб. 14 580 руб. 1,4 куб. м/ч 5,5 руб./куб. м
Электр. отопление 15 000 руб. 13 000 руб. 5,5 (кВтч) 3,8 руб./(кВтч)
Обдумав оба варианта, хозяин решил установить газовое отопление. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разницу в стоимости покупки и установки газового и электрического оборудования?
Ответ: 650
6. Найдите значение выражения 4,7 − 8,2.
Решение:
Вычитаем из меньшего по модулю число большее по модулю и ставим знак минус:
8,2 − 4,7 = 3,5
Значит, 4,7 − 8,2 = −3,5
Ответ: −3,5
7. Между какими целыми числами заключено число 172/15?
1) 9 и 10
2) 10 и 11
3) 11 и 12 +
4) 12 и 13
Решение:
Разделим 172 на 15:
172 : 15 = 11,4666…
Это число больше 11, но меньше 12.
8. Найдите значение выражения √5 · 12 · √15
Решение:
Перемножим подкоренные выражения:
√5 · √15 = √(5 · 15) = √75
Теперь умножим на 12: 12 · √75
Упростим √75 = √(25 · 3) = 5√3
Получаем: 12 · 5√3 = 60√3
Ответ: 60√3
9. Решите уравнение 𝑥2 − 4 = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решение:
Это уравнение разности квадратов:
(𝑥 − 2)(𝑥 + 2) = 0
Корни: 𝑥 = 2 и 𝑥 = −2
Меньший корень: −2
Ответ: −2
10. На тарелке лежат одинаковые на вид пирожки: 3 с капустой, 8 с рисом и 1 с луком и яйцом. Игорь наугад берёт один пирожок. Найдите вероятность того, что пирожок окажется с капустой.
Решение:
Всего пирожков: 3 + 8 + 1 = 12
Благоприятных исходов (пирожков с капустой): 3
Вероятность P = 3/12 = 1/4 = 0,25
Ответ: 0,25
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 + 𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏.
КОЭФФИЦИЕНТЫ
1) 𝑘 < 0, 𝑏 < 0
2) 𝑘 < 0, 𝑏 > 0
3) 𝑘 > 0, 𝑏 > 0
В таблице под каждой буквой укажите соответствующий номер.
Ответ: А)2 Б)3 В)1 ?
12. Закон Джоуля–Ленца можно записать в виде 𝑄 = 𝐼2𝑅𝑡, где 𝑄 — количество теплоты (в джоулях), 𝐼 — сила тока (в амперах), 𝑅 — сопротивление цепи (в омах), а 𝑡 — время (в секундах). Пользуясь этой формулой, найдите сопротивление цепи 𝑅 (в омах), если 𝑄 = 81 Дж, 𝐼 = 1,5 A, 𝑡 = 9 с.
Решение:
Формула: 𝑄 = 𝐼²𝑅𝑡
Выразим R: R = 𝑄 / (𝐼²𝑡)
Подставим значения:
R = 81 / ( (1,5)² · 9 ) = 81 / (2,25 · 9) = 81 / 20,25 = 4
Ответ: 4
13. Укажите решение неравенства 2𝑥 − 8 ≥ 4𝑥 + 6.
1) (−∞; − 7] +
2) (−∞; 1];
3) [1; + ∞;
4) [−7; + ∞)
Решение:
Перенесем все члены с x влево, а числа вправо:
2𝑥 − 4𝑥 ≥ 6 + 8
−2𝑥 ≥ 14
Разделим на отрицательное число (-2), при этом знак неравенства меняется на противоположный:
𝑥 ≤ −7
Это интервал (−∞; −7]
Ответ: 1) (−∞; −7]
14. В ходе бета-распада радиоактивного изотопа А каждые 8 минут половина его атомов без потери массы преобразуются в атомы стабильного изотопа Б.
В начальный момент масса изотопа А составляла 480 мг. Найдите массу образовавшегося изотопа Б через 32 минут. Ответ дайте в миллиграммах.
Решение:
Период полураспада (превращения половины атомов А в Б) = 8 минут.
Время 32 минуты = 32 / 8 = 4 периода.
Начальная масса А = 480 мг.
После 1-го периода: масса А = 480 / 2 = 240 мг. Масса Б = 240 мг.
После 2-го периода: масса А = 240 / 2 = 120 мг. Масса Б = 240 (уже было) + 120 (новые) = 360 мг.
После 3-го периода: масса А = 120 / 2 = 60 мг. Масса Б = 360 + 60 = 420 мг.
После 4-го периода: масса А = 60 / 2 = 30 мг. Масса Б = 420 + 30 = 450 мг.
Масса изотопа Б через 32 минуты равна 450 мг.
Ответ: 450
15. Два катета прямоугольного треугольника равны 4 и 11.
Найдите площадь этого треугольника.
Решение:
S = (1/2) · 4 · 11 = 2 · 11 = 22
Ответ: 22
16. Радиус окружности, вписанной в равносторонний треугольник, равен 15. Найдите высоту этого треугольника.
Решение:
Радиус вписанной окружности (r) и высоту (h): r = h / 3.
Выразим h: h = 3r = 3 · 15 = 45.
Ответ: 45
17. Один из углов ромба равен 127°. Найдите меньший угол этого ромба.
Ответ дайте в градусах.
Решение:
Угол, смежный с углом в 127°, равен 180° − 127° = 53°.
Противоположные углы ромба равны. Значит, углы ромба: 127°, 53°, 127°, 53°.
Меньший угол равен 53°.
Ответ: 53
18. Какое из следующих утверждений является истинным высказыванием?
1) Диагонали ромба точкой пересечения делятся пополам. +
2) В тупоугольном треугольнике все углы тупые.
3) Каждая из биссектрис равнобедренного треугольника является его высотой.
В ответe запишите номер истинного высказывания.
19. Первые 200 км автомобиль ехал со скоростью 50 км/ч, следующие 320 км — со скоростью 80 км/ч, а последние 140 км — со скоростью 35 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Решение:
Общее расстояние = 200 км + 320 км + 140 км = 660 км
Время на первом участке: t1 = расстояние / скорость = 200 км / 50 км/ч = 4 часа
Время на втором участке: t2 = расстояние / скорость = 320 км / 80 км/ч = 4 часа
Время на третьем участке: t3 = расстояние / скорость = 140 км / 35 км/ч = 4 часа
Общее время = t1 + t2 + t3 = 4 часа + 4 часа + 4 часа = 12 часов
Средняя скорость = Общее расстояние / Общее время = 660 км / 12 часов = 55 км/ч
Ответ: Средняя скорость автомобиля на протяжении всего пути составляет 55 км/ч.
20. Боковые стороны AB и CD трапеции ABCD равны соответственно 8 и 10, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB . Найдите площадь трапеции.
Ответ: площадь трапеции равна 40
