5 класс. Олимпиада по математике (ЯКласс 2 тур) 10-15 апреля 2025, какие ответы на задачи?

Те ребята, которые прошли олимпиаду первого тура и набрали хотя бы 50% верных ответов, прошли во второй тур. Который состоялся сегодня 10 апреля. Ответы на второй тур будут известны не раньше 15 апреля. Мы тоже прошли олимпиаду и здесь поделимся заданиями и нашими ответами. Хочется заметить, что у нас заработано баллов: 75 / 80. Значит где-то есть ошибка. Поэтому не опирайтесь на наши ответы, а решайте по началу самостоятельно. Ну, а теперь переходим к заданиям:

1. В течение одной недели, включая выходные дни, ученики класса участвовали в весёлой школьной
акции: каждый день каждый ученик писал одну записку с комплиментом (можно было написать комплимент
себе, однокласснику или классному руководителю). В итоге у каждого ученика накопилось по 2 полученные
записки, а у классного руководителя — 200 записок. Сколько учеников в классе?
Решение:
Пусть количество учеников в классе равно x.
Всего за неделю было написано 7x записок (так как каждый из x учеников писал по одной записке каждый из 7 дней).
Также была написана какая-то часть записок классному руководителю.
Общее количество полученных учениками записок равно 2x (так как каждый из x учеников получил по 2 записки).
Всего было написано 2x + 200 записок.
Таким образом, мы можем составить уравнение:
7x = 2x + 200
Решаем уравнение:
7x — 2x = 200
5x = 200
x = 200 / 5
x = 40
Ответ: 40 учеников.

2. Четыре мудреца пришли к императору, чтобы назвать секретную последовательность из трёх букв. Три мудреца всегда говорят правду, а один всегда лжёт. Фразы мудрецов представлены ниже.
Платонус: «Все буквы последовательности разные».
Сократус: «Первая буква — А».
Эпикурус: «Вторая буква — Б».
Диогенус: «Третья буква — В».+
Платонус: «Буквы в последовательности расположены по алфавиту».
Кто из мудрецов является лжецом?
Решение:
Если Платонус лжет: Это означает, что либо не все буквы разные, либо они не расположены по алфавиту, либо и то, и другое.
Если Сократус лжет: Первая буква НЕ «А».
Если Эпикурус лжет: Вторая буква НЕ «Б».
Если Диогенус лжет: Третья буква НЕ «В».
Теперь проанализируем, какие комбинации возможны, если считать, что только один лжет:
Предположим, лжет Платонус: Тогда последовательность типа АБВ невозможна, так как буквы должны быть разными и по алфавиту. Но она может быть, например, ААБ (две одинаковые буквы) или АБГ (не по алфавиту).
Предположим, лжет Сократус: Тогда первая буква не «А». Значит, если Эпикурус и Диогенус говорят правду, последовательность выглядит как XБВ (где X — не А). Но тогда Платонус говорит правду, что все буквы разные и по алфавиту. Это противоречит условию, что только один лжет.
Предположим, лжет Эпикурус: Тогда вторая буква не «Б». Последовательность выглядит как АXВ (где X — не Б). Тогда Платонус говорит правду, что все буквы разные и по алфавиту. Это возможно, например, АГВ – невозможно, т.к. не по алфавиту. Все буквы разные и по алфавиту, значит, Платонус говорит правду. Противоречие.
Предположим, лжет Диогенус: Тогда третья буква не «В». Последовательность выглядит как АБX (где X — не В). Тогда Платонус говорит правду, что все буквы разные и по алфавиту. Это возможно, например, АБГ.
Итак, единственная ситуация, которая не приводит к противоречию – это когда лжет Диогенус. В этом случае последовательность может быть, например, АБГ.
Ответ: лжец — Диогенус

3. В университете города Тучекукуевск всего 80 студентов, учащихся на трёх факультетах: медицинском,
философском и физическом, причём физиков вдвое больше, чем философов. В честь сданных экзаменов все
студенты решили подарить друг другу подарки.
Каждый философ получил на 1 подарок меньше, чем подарил.
Каждый физик получил на 2 подарка меньше, чем подарил.
Каждый медик получил на 5 подарков больше, чем подарил.
Найди количество философов.
Решение:
Пусть:
Pf — количество подарков, подаренных философами
Pm — количество подарков, подаренных медиками
Pp — количество подарков, подаренных физиками
Rf — количество подарков, полученных философами
Rm — количество подарков, полученных медиками
Rp — количество подарков, полученных физиками
Тогда:
Pf + Pm + Pp = Rf + Rm + Rp = 6320
Из условий про разницу между полученными и подаренными подарками мы знаем:
Rf = Pf — f
Rm = Pm + 5m
Rp = Pp — 2p
Подставим эти выражения в уравнение Rf + Rm + Rp = Pf + Pm + Pp:
(Pf — f) + (Pm + 5m) + (Pp — 2p) = Pf + Pm + Pp
-f + 5m — 2p = 0
Теперь подставим p = 2f и m = 80 — 3f в последнее уравнение:
-f + 5(80 — 3f) — 2(2f) = 0
-f + 400 — 15f — 4f = 0
-20f + 400 = 0
20f = 400
f = 20
Следовательно, количество философов равно 20.
Ответ: 20

4. Семь братьев-волшебников сели за праздничный стол по кругу. Известно, что каждый брат всегда говорит
правду старшему, а младшему — всегда лжёт. Каждый волшебник сказал своему соседу справа: «Здесь все мне
врут». Рассади волшебников в правильном порядке.

Варианты ответов:
Лё — 378 лет
Ла — 299 лет
Лю — 446 лет
Ли — 250 лет
Ло — 190 лет

Здесь явная описка или ошибка в задаче. Так как в условии задачи говориться о семи братьях, но их всего 6. Поэтому как рассадить 7 братьев на 5 мест, непонятно и где еще один брат, который не указан (имя) в задаче, тоже непонятно.

Мы не стали менять условие задачи, но решали задачу из расчета — 6 братьев. После долгих анализов, проверок и решений (примерно так:)
Каждый брат лжёт своему соседу справа, а значит, сосед справа младше его.
Из вывода следует, что каждый следующий брат (по часовой стрелке) младше предыдущего.
Поскольку Лу (105 лет) — младший, то слева от него должен сидеть старший брат, а дальше по убыванию возраста. Но у нас есть старший брат — Лю (446 лет). Проверим, может ли он сидеть слева от Лу:
Если Лю сидит слева от Лу, то следующий (по часовой стрелке) после Лю — Лу. Но Лю (446) старше Лу (105), и по правилам Лю должен лгать Лу (потому что Лу младше).
Это согласуется с нашим выводом.
Теперь продолжим цепочку по убыванию возраста (каждый следующий младше предыдущего):
Лю (446) → Лё (378) → Ла (299) → Ли (250) → Ло (190) → Лу (105) → Лю (446)
Проверим:
Лю говорит Лё: Лё младше (378 < 446) ⇒ Лю лжёт Лё (верно).
Лё говорит Ла: Ла младше (299 < 378) ⇒ Лё лжёт Ла (верно).
Ла говорит Ли: Ли младше (250 < 299) ⇒ Ла лжёт Ли (верно).
Ли говорит Ло: Ло младше (190 < 250) ⇒ Ли лжёт Ло (верно).
Ло говорит Лу: Лу младше (105 < 190) ⇒ Ло лжёт Лу (верно).
Лу говорит Лю: Лю старше (446 > 105) ⇒ Лу должен говорить правду Лю.
Но по условию каждый говорит соседу справа «Все мне врут», и мы уже выяснили, что эта фраза не может быть правдой.
⇒ Противоречие ⇒ Лу не может говорить правду Лю.
Значит, Лю не может сидеть слева от Лу….

У нас получился такой ответ:

5. На занятии по оригами Маша разрезала лист в клетку размером 8 х 8 на 11 прямоугольников (разрезания
строго по сторонам клеток). Длины сторон всех прямоугольников после всех разрезаний оказались больше 1.
Найди минимальный периметр из всех периметров получившихся фигур.
Ответ: 8

Здесь в этой задачке, поэкспериментировав с различными комбинациями, мы пришли к такому решению:
8 прямоугольников 2×2 (площадь 32, периметр 64)
3 прямоугольника 2×4 (площадь 24, периметр 36)
Сумма площадей 32 + 24 + 8 = 64.
Сумма периметров = 64 + 36 = 100
Потому, что минимальный периметр, который можно получить, равен 100.
Конечно задача требует некоторого перебора и интуиции. Важно понять, что прямоугольники, наиболее близкие к квадратам, дают минимальный периметр при заданной площади.

6. В субботу коала Малышка съедает 2 кг эвкалипта, в воскресенье — 5 кг, а в остальные дни по 1 кг. В
новогоднюю ночь Малышка посчитала, что за год съела 629 кг эвкалипта. Какой день недели придётся на
первое января?
Ответ:
Понедельние
вторник
среда
четверг
пятница
суббота
воскресенье +

Решение:
Рассчитаем потребление эвкалипта за неделю:
Суббота: 2 кг
Воскресенье: 5 кг
Остальные 5 дней: 5 * 1 кг = 5 кг
Всего за неделю: 2 + 5 + 5 = 12 кг
Определим количество полных недель в году:
В году 52 недели.
Рассчитаем потребление эвкалипта за полные недели:
52 недели * 12 кг/неделя = 624 кг
Рассчитаем потребление эвкалипта за неполную неделю:
Всего съедено за год: 629 кг
Съедено за полные недели: 624 кг
Съедено за неполную неделю: 629 — 624 = 5 кг
Определим день недели, с которого начинается год:
В неполную неделю съедено 5 кг эвкалипта. Это соответствует воскресенью (5 кг). Значит, 1 января было воскресенье.
Ответ: Понедельник 

7. Отберём случайным образом 27 различных натуральных нечётных чисел, меньших 100. Найди,
какое минимальное количество пар с суммой 102 может быть среди выбранных чисел.
Ответ: Минимальное количество пар с суммой 102 = 1

8. Найди наибольшее количество тетрамино (см. рис. 1), которые можно разместить на клетчатой доске размером 7 х 7 без перекрытий.

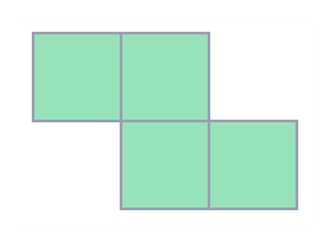
Ответ: 9

9. На футбольный матч пришли 30 человек — это математики и их друзья-информатики.
Некоторые математики пришли одни, а некоторые взяли с собой по одному другу-информатику. Известно, что
математиков, пришедших без друзей, было на 10 меньше, чем тех, кто пришёл с информатиками.
Также известно:
один информатик может дружить с несколькими математиками,
один математик — не более чем с одним информатиком.
Сколько всего могло быть информатиков, приведённых на матч? Перечисли все возможные варианты.
Варианты ответов:
1-2-3-4-5-6-7-8-9-10-11-12-13-14-15

Ответ: 2​,4​,6​,8​,10​,12​

10. Петя выписывает все четырёхзначные числа, у которых ни одна из цифр не делится на 3. Найди сумму всех цифр для чисел, выписанных Петей. (Число в ответе запиши без пробелов.)

Ответ: 23328