1 Ответ
Задание 1. Найдите значение выражения 12sin75*cos75*cos25/sin(-115)
Решение:
Преобразуем числитель, используя формулу двойного угла:
12sin(75°)cos(75°)cos(25°) = 6 * 2sin(75°)cos(75°)cos(25°) = 6sin(150°)cos(25°)
Упростим sin(150°). Т.к. sin(150°) = sin(180° — 30°) = sin(30°) = 1/2, то:
6sin(150°)cos(25°) = 6 * (1/2) * cos(25°) = 3cos(25°)
Преобразуем знаменатель:
sin(-115°) = -sin(115°) = -sin(90° + 25°) = -cos(25°)
Теперь подставим упрощенные числитель и знаменатель в исходное выражение:
3cos(25°) / -cos(25°) = -3
Ответ: -3
Задание 2. В правильной четырёхугольной пирамиде SABCD сторона основания AB равна 18, а боковое ребро AS равно 15. Найдите синус угла между прямыми AB и SD.
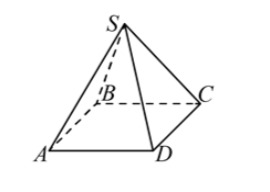
Ответ: 0,8
Задание 3. Укажите номера всех графов, в которых существует эйлеров путь, то есть путь, соединяющий все вершины графа и проходящий через каждое ребро ровно по одному разу.

Ответ: 2, 4
Задание 4. Какое из утверждений неверно?
Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
Через любую точку пространства проходит бесконечно много прямых, перпендикулярных данной прямой.
Если плоскость перпендикулярна одной из двух перпендикулярных плоскостей, то она параллельна другой плоскости. +
Задание 5. Найдите количество элементов множества (B◡C)◠A, где:
A – множество двузначных натуральных чисел,
B – множество чисел, не кратных числу 3,
C – множество чисел, кратных числу 4.
Ответ: 68
Задание 6. Решите уравнение log_4(2-x)^3+4log_8(2-x)=8,5. Если уравнение имеет больше одного корня, в ответ запишите сумму всех его корней.
Решение:
Преобразуем уравнение, используя свойства логарифмов:
log_4(2-x)^3 = 3 * log_4(2-x)
log_8(2-x) = log_2(2-x) / log_2(8) = log_2(2-x) / 3
Подставим эти преобразования в исходное уравнение:
3 * log_4(2-x) + 4 * (log_2(2-x) / 3) = 8.5
Заметим, что log_4(2-x) = log_2(2-x) / log_2(4) = log_2(2-x) / 2. Подставим это в уравнение:
3 * (log_2(2-x) / 2) + 4 * (log_2(2-x) / 3) = 8.5
Обозначим y = log_2(2-x). Тогда уравнение примет вид:
(3/2) * y + (4/3) * y = 8.5
Приведем к общему знаменателю и сложим:
(9/6) * y + (8/6) * y = 8.5
(17/6) * y = 8.5
y = 8.5 * (6/17) = (17/2) * (6/17) = 3
Теперь найдем x, зная, что y = log_2(2-x) = 3:
2^3 = 2-x
8 = 2-x
x = 2 — 8 = -6
Проверим, что x = -6 удовлетворяет условию 2-x > 0:
2 — (-6) = 8 > 0. Условие выполнено.
Уравнение имеет только один корень: x = -6.
Сумма корней (если их несколько) равна -6.
Ответ: -6
Задание 7. В прямоугольном параллелепипеде ABCDA1B1C1D1 точка K – середина ребра B1C1, AB = 11, AD = 4√11, AA1 = 3√22. Найдите расстояние от точки A1 до плоскости CDK.

Ответ: 6
Задание 8. Решите уравнение 4*9^x+0,5+9*4^x+0,5=35*6^x. Если уравнение имеет больше одного корня, в ответ запишите сумму корней.
Ответ: Сумма корней: 2+(−1) =1
Задание 10. На одной полке стоит 36 блюдец: 14 синих и 22 красных. На другой полке стоит 36 чашек: 27 синих и 9 красных. Наугад берут два блюдца и две чашки. Найдите вероятность, что из них можно будет составить две чайные пары (блюдце с чашкой), каждая из которых будет одного цвета.
Ответ: 0,29
