1-5 класс. Олимпиада «От звёздочек – к звёздам!» по математике 2025, какие вопросы и ответы?

1 класс:

1. На клумбе расцвели два цветка. Каждый день распускаются 3 новых цветка, а один – вянет. Сколько распустившихся цветов будет на клумбе через 3 дня?

Решение:

1. Определим изменение количества цветков за один день:
   • Новые цветы: +3
   • Увядшие цветы: -1
   • Итого за день: 3−1=+2 цветка
2. Рассчитаем общее изменение за 3 дня:
   • За один день добавляется 2 цветка.
   • За три дня: 2×3=6 цветков
3. Найдем общее количество цветков через 3 дня:
   • Изначально было 2 цветка.
   • Добавилось 6 цветков.
   • Итого: 2+6=8 цветков

Ответ: 8 

2. Аня – самая высокая; Катя – ниже всех остальных; рядом с Катей – Вова; рядом с Петей
– Даша. Как зовут ребёнка под номером 1?

Аня самая высокая — 5
Катя ниже всех — 4
Вова рядом с Катей — 3
Значит второй мальчик не может Вовой, его зовут Петя и он стоит рядом с девочкой по имени Даша. Значит ребенка под номером 1 зовут — Даша.

3. По китайскому календарю 2025 год – год Змеи. В одном зоопарке живёт удивительная змея. По всей длине туловища у неё изображены числа в определённой последовательности. Какое число должно быть на месте вопроса?

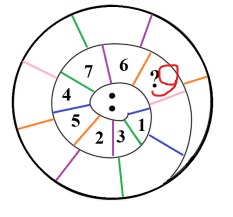
4. На клетчатой бумаге Петя нарисовал линии. Какая линия самая длинная. Укажите её номер?

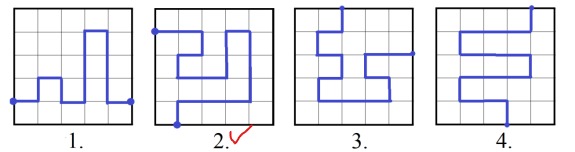
5. Прочитайте слово. (Начинайте читать с самой большой буквы, а заканчивайте – самой маленькой).

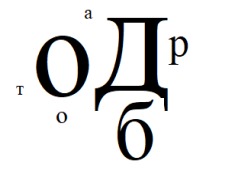
Ответ: это слово — доброта

2 класс:

1. Из карточек, на которых написаны цифры 1, 2, 3, и 4, Знайка составил два двузначных числа. Оказалось, что разность этих двузначных чисел принимает самое маленькое возможное значение. Чему равна эта разность?
Решение:
Используя цифры 1, 2, 3, 4, можно составить следующие двузначные числа: 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43.
Нам нужно найти два числа из этого списка, разность между которыми минимальна. Очевидно, что числа должны начинаться с соседних цифр (например, 2 и 3). Рассмотрим варианты:
Числа, начинающиеся с 2 и 3: 21, 23, 24 и 31, 32, 34.
Разность |31 — 24| = 7, разность |32 — 24| = 8, разность |31 — 23| = 8, разность |32 — 21| = 11.
Числа, начинающиеся с 1 и 2: 12, 13, 14 и 21, 23, 24.
Разность |21-14| = 7, разность |23-14| = 9, разность |21-13| = 8, разность |21-12| = 9
Числа, начинающиеся с 3 и 4: 31, 32, 34 и 41, 42, 43.
Разность |41-34| = 7, разность |42-31| = 11.
Лучший вариант – числа 31 и 24 (или 41 и 34), разность между которыми равна 7.
Другой способ: Чтобы получить минимальную разность, нужно чтобы десятки были как можно ближе, а единицы как можно дальше друг от друга. Берем числа 31 и 24. Разность: 31 — 24 = 7.
Ответ: 7.

2. Первые весы находятся в равновесии. Сколько яблок надо положить на пустую чашу вторых весов, чтобы их уравновесить?

Ответ: На первых весах мы видим, что 3 груши весят как 4 яблока и 1 груша. Значит каждая груша весит 2 яблока. Таким образом, на вторые весы, чтобы вес был равный надо положить 2 яблока.

3. Сумма чисел на всех лучиках каждой звёздочки равна 25. Одно число закрыто. Какое число следует поставить вместо вопроса?

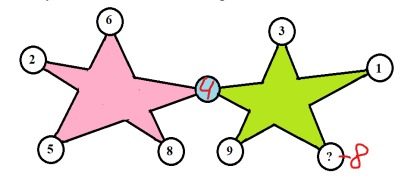
4. Знайка занимается прыжками в воду с трамплина. Когда Знайка прыгает с трамплина, то сначала трамплин подбрасывает его вверх на 1 метр, а затем Знайка летит на 6 метров вниз, попадая в воду. После он поднимается вверх на 2 метра до поверхности воды. На какой высоте над водой находится трамплин?
Решение:

1. Знайка находится на трамплине.
2. Трамплин подбрасывает его на 1 метр вверх от уровня трамплина.
3. Затем Знайка летит на 6 метров вниз от наивысшей точки прыжка и оказывается в воде.
4. Из воды Знайка поднимается на 2 метра до поверхности воды.

Таким образом, расстояние от наивысшей точки прыжка до поверхности воды составляет 6 — 2 = 4 метра. Так как трамплин подбрасывает Знайку на 1 метр вверх, высота трамплина над водой равна 4 — 1 = 3 метра.

Ответ: 3 метра

5. Большой кубик склеен из маленьких кубиков, как показано на рисунке. В нём просверлили 3 дырки насквозь вдоль граней большого кубика. Сколько маленьких кубиков осталось неповреждёнными?

Решение:

1. Подсчитаем общее количество удалённых кубиков — 27
   • Первая дырка удаляет 3 кубика.
   • Вторая дырка удаляет 2 новых кубика (один уже удалён первой дыркой).
   • Третья дырка удаляет 3 новых кубика (один уже удалён первой и второй дырками)
   • Итого удалено: 3+2+3=8 кубиков.
2. Найдем количество неповреждённых кубиков:
   • Изначально было 27 кубиков.
   • Удалено 8 кубиков.
   • Осталось: 27−8=19 кубиков.

Ответ: 19 кубиков не повреждены. 

3-4 класс:

1. На каждой звёздочке написаны числа. На второй и третьей звёздочке пропущено по одному числу. Вставьте пропущенные числа так, чтобы сумма чисел на первой звёздочке была меньше, чем сумма чисел на второй, а сумма чисел на третьей звёздочке была больше, чем на второй. И при этом поставленные числа были наименьшими возможными. В ответ запишите, какие числа Вы поставили.

2. Из карточек, на которых написаны цифры 0, 2, 4, 5, 6 и 7, Знайка составил два трёхзначных
числа. Оказалось, что разность этих трёхзначных чисел принимает самое маленькое возможное значение. Чему равна эта разность? Карточки запрещено переворачивать.
Решение:
Чтобы разность двух трёхзначных чисел была минимальной, нужно, чтобы числа были максимально близки друг к другу. Это значит, что их первые цифры (сотни) должны быть как можно более похожими.
Самые маленькие цифры из набора — 0, 2, 4, 5, 6 и 7. Ноль не может быть первой цифрой, поэтому будем использовать 2 и 4.
Чтобы разница была минимальной, возьмём в качестве сотен числа 4 и 5. Тогда числа будут выглядеть как 5XY и 4ZW. Теперь нужно, чтобы 5XY было как можно меньше, а 4ZW как можно больше. Для этого X и Z должны быть как можно ближе друг к другу. Лучшим вариантом будет разместить оставшиеся цифры так, чтобы получилось 502 и 476.
Тогда разница будет 502-476 = 26.
Если мы поменяем цифры и сделаем 406 и 572, то разница станет гораздо больше.
Таким образом, минимальная разность достигается, когда мы составляем числа 502 и 476.
Разность равна 502 — 476 = 26.
Ответ: 26.

 

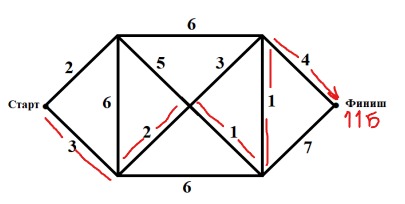
3. Незнайка участвует в соревнованиях по бегу с барьерами. На рисунке показаны дорожки стадиона и
количество барьеров на каждой дорожке. Незнайка выбирает такой путь, чтобы ему пришлось перепрыгивать наименьшее количество барьеров. Сколько барьеров преодолел Незнайка?

4. Знайка решил готовиться к олимпиаде «От Звёздочек – к Звёздам» по математике. Он придумал план, по которому каждый день недели будет решать разное количество задач, кроме тех дней, когда у него тренировки. Знайка тренируется в четверг и пятницу, и он запланировал, что в эти дни будет решать одинаковое количество задач. Семь дней подряд Знайка придерживался своего плана. В первые шесть дней выполнения плана он решал по 5, 3, 2, 4, 7 и 6 задач соответственно.
Сколько задач он решил на седьмой день плана?
Решение:
Допустим, он принял это решение в субботу. Тогда:
Сб — 5 задач
Вс — 3 задачи
Пн — 2 задачи
Вт — 4 задачи
Ср — 7 задач
Чт — 6 задач
Пт — 6 задач
На седьмой день плана Знайка решил 6 задач.

5. Знайка занимается прыжками в воду с трамплина. Когда Знайка прыгает с трамплина, то сначала трамплин подбрасывает его вверх на 1 метр, а затем Знайка летит на 6 метров вниз, попадая в воду. После он поднимается вверх на 2 метра до поверхности воды. На какой высоте над водой находится трамплин?
Ответ смотрите в задачке за 2 класс! 

5 класс:

1. По китайскому календарю 2025 год является годом Змеи. В одном зоопарке живёт удивительная змея. Она очень длинная, а её туловище имеет трёхцветную раскраску. Начиная от головы, змея имеет полоски зелёного, жёлтого и красного цветов, которые постоянно повторяются по всей длине змеи: зелёный, жёлтый, красный, зелёный, жёлтый, красный и так далее.

Какого цвета будет у змеи 2025 полоска?

Решение:

1. Определим последовательность цветов:
   • 1-я полоска: зелёный
   • 2-я полоска: жёлтый
   • 3-я полоска: красный
   • 4-я полоска: зелёный
   • 5-я полоска: жёлтый
   • 6-я полоска: красный
   • и так далее…
2. Заметим, что цвета повторяются каждые 3 полоски:
   • Это значит, что последовательность имеет цикл длиной 3.
3. Найдём, к какому циклу относится 2025-я полоска:
   • Для этого разделим 2025 на 3 и найдём остаток:2025÷3=675 с остатком 0
   • Остаток 0 означает, что 2025-я полоска соответствует последнему цвету в цикле.
4. Определим цвет:
   • В цикле из трёх цветов (зелёный, жёлтый, красный), последний цвет — красный.

Ответ: красная 

2. Пятиклассники праздновали Новый год и вместе съели 105 конфет. Причём каждая девочка съела по 4 конфеты, а каждый мальчик по 5 конфет. Сколько детей учатся в классе, если девочек больше, чем мальчиков, но меньше, чем 20 человек?
Решение:
Если b = 1, то d = (105 — 5) / 4 = 100 / 4 = 25. Но d > 20, поэтому не подходит.
Если b = 2, то d = (105 — 10) / 4 = 95 / 4 = 23.75 (не целое).
Если b = 3, то d = (105 — 15) / 4 = 90 / 4 = 22.5 (не целое).
Если b = 4, то d = (105 — 20) / 4 = 85 / 4 = 21.25 (не целое).
Если b = 5, то d = (105 — 25) / 4 = 80 / 4 = 20. Но d не меньше 20, поэтому не подходит.
Если b = 6, то d = (105 — 30) / 4 = 75 / 4 = 18.75 (не целое).
Если b = 7, то d = (105 — 35) / 4 = 70 / 4 = 17.5 (не целое).
Если b = 8, то d = (105 — 40) / 4 = 65 / 4 = 16.25 (не целое).
Если b = 9, то d = (105 — 45) / 4 = 60 / 4 = 15. Здесь d = 15, b = 9. d > b и d < 20. Подходит!
Если b = 10, то d = (105 — 50)/4 = 55/4 = 13.75 (не целое).
Если b = 11, то d = (105 — 55)/4 = 50/4 = 12.5 (не целое).
Если b = 12, то d = (105 — 60)/4 = 45/4 = 11.25 (не целое).
Если b = 13, то d = (105 — 65)/4 = 40/4 = 10. Здесь d = 10, b = 13, но d < b, поэтому не подходит.
Единственное решение, удовлетворяющее всем условиям, это d = 15 и b = 9.
Общее количество детей в классе: d + b = 15 + 9 = 24.
Ответ: В классе учатся 24 ученика.

3. Число 2025 имеет 15 целых делителей, включая 1 и само число 2025. Пятиклассник Вова нашёл все делители и расположил их в порядке возрастания, начиная с 1 и заканчивая 2025. Какой делитель одиннадцатый по порядку, считая от 1?
Решение:
Для начала, давайте найдем разложение числа 2025 на простые множители. 2025=25⋅81=52⋅34 Число целых делителей равно (2+1)(4+1)=3⋅5=15. Все делители числа 2025: 3a⋅5b, где 0≤a≤4 и 0≤b≤2. Расположим их в порядке возрастания:
30⋅50=1
31⋅50=3
32⋅50=9
33⋅50=27
34⋅50=81
30⋅51=5
31⋅51=15
32⋅51=45
33⋅51=135
34⋅51=405
30⋅52=25
31⋅52=75
32⋅52=225
33⋅52=675
34⋅52=2025 Сортируем полученные числа в порядке возрастания: 1, 3, 5, 9, 15, 25, 27, 45, 75, 81, 135, 225, 405, 675, 2025 Одиннадцатый по порядку делитель равен 135.

4. Пятиклассник Миша решил готовиться к олимпиаде «От Звёздочек – к Звёздам» по математике. Он придумал план, по которому каждый день недели будет решать разное количество задач, кроме тех дней, когда у него тренировки. Миша тренируется в четверг и пятницу, и он запланировал, что в эти дни будет решать одинаковое количество задач. Семь дней подряд Миша придерживался своего плана. В первые шесть дней выполнения плана он решал по 5, 3, 2, 4, 7 и 6 задач соответственно. Сколько задач он решил на седьмой день плана?
Ответ смотрите на аналогичную задачку за 3-4 класс! 

5. Три друга Миша, Петя и Вова бежали одну дистанцию наперегонки. Миша бежал с одной и той же скоростью всю дистанцию, Петя первую половину пути бежал вдвое быстрее, чем Миша, а вторую половину пути – вдвое медленнее, чем Миша. Вова первую треть пути бежал втрое быстрее Миши, вторую треть пути в два раза медленнее Миши, а третью часть в два раза быстрее Миши. Кто из мальчиков пришёл вторым к финишу? В ответ запишите его имя.
Решение:
Чтобы решить эту задачу, нужно сравнить время, которое каждый мальчик потратил на всю дистанцию. Мы не знаем длину дистанции, поэтому можем представить её как единицу (1). Также мы можем представить скорость Миши как единицу (1).
Миша:
Скорость: 1
Время: 1 / 1 = 1 (вся дистанция / скорость)
Петя:
Первая половина пути:
Скорость: 1 * 2 = 2
Расстояние: 1 / 2 = 0.5
Время: 0.5 / 2 = 0.25
Вторая половина пути:
Скорость: 1 / 2 = 0.5
Расстояние: 1 / 2 = 0.5
Время: 0.5 / 0.5 = 1
Общее время Пети: 0.25 + 1 = 1.25
Вова:
Первая треть пути:
Скорость: 1 * 3 = 3
Расстояние: 1 / 3 ≈ 0.33
Время: 0.33 / 3 ≈ 0.11
Вторая треть пути:
Скорость: 1 / 2 = 0.5
Расстояние: 1 / 3 ≈ 0.33
Время: 0.33 / 0.5 ≈ 0.66
Третья треть пути:
Скорость: 1 * 2 = 2
Расстояние: 1 / 3 ≈ 0.33
Время: 0.33 / 2 ≈ 0.165
Общее время Вовы: 0.11 + 0.66 + 0.165 ≈ 0.935
Теперь сравним времена:
Миша: 1
Петя: 1.25
Вова: 0.935
Вова потратил меньше всего времени, значит, он прибежал первым. Миша прибежал вторым, а Петя последним.
Ответ: Миша