1 Ответ
1. Змейка
Успешно решив раньше времени контрольную работу по математике, Тимофей выбрал на клетчатой бумаге квадрат со стороной n клеток и стал заполнять его «змейкой» от левого верхнего угла так, как показано на рисунке. Определите длину проведённых линий.
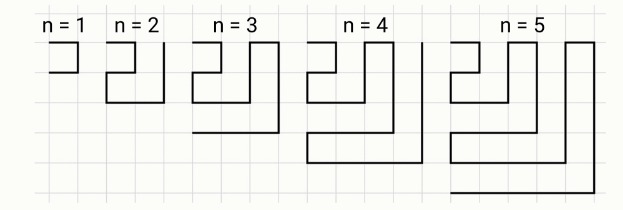
Формат входных данных:
Единственная строка входных данных содержит натуральное число n (1≤n≤10^9).
Формат выходных данных:
Выведите одно натуральное число — ответ на вопрос задачи.
Обратите внимание, что значение ответа в этой задаче может превышать возможное значение 32‑битной целочисленной переменной, поэтому необходимо использовать 64‑битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Система оценки
Решения, правильно работающие при n≤10^4, будут оцениваться в 40 баллов.
Ввод — 1, 5
Вывод — 3, 35
2. Две сестры
Аполлинария Прокофьевна и Белла Прокофьевна — две сестры‑пенсионерки. Аполлинарии Прокофьевне каждый день необходимо принимать одну таблетку от забывчивости. К сожалению, этот режим она не соблюдает и вспоминает о лекарстве только раз в a дней (то есть приняв лекарство сначала в первый день, в следующий раз она примет его в день номер 1+a). Белле Прокофьевне каждый день необходимо принимать одну таблетку от жадности. Ко всеобщему огорчению, и её болезнь сильнее лекарства, поэтому каждый день она глотает b таблеток. Внешне эти таблетки выглядят совершенно одинаково и каждая из сестёр считает, что вот этот пузырёк с n пилюлями именно её. На сколько дней им хватит этого количества лекарств?
Три строки входных данных содержат три целых числа a, b (1≤a,b≤100) и n(1≤n≤10^18).
Замечание
В первом примере Аполлинария Прокофьевна принимает по одной таблетке раз в два дня (начиная с первого), Белла Прокофьевна принимает по три таблетки каждый день. В пузырьке 12 таблеток.
В первый день Аполлинария принимает одну таблетку, а Белла — три. В пузырьке осталось восемь пилюль.
Во второй день Аполлинария забывает принять таблетку, а Белла опять съедает три. В пузырьке осталось пять пилюль.
В третий день Аполлинария принимает одну таблетку, а Белла — три. В пузырьке осталась последняя пилюля, ещё на один день этого количества сёстрам не хватит.
Во втором примере начального количества таблеток не хватит даже на один день.
Ввод -2, 3, 12
Вывод — 3
Решение:
При заданных условиях следует считать, что каждый день одна таблетка уходит на Аполлинарию Прокофьевну раз в a дней и каждый день уходит b таблеток на Беллу Прокофьевну. Для определения, сколько дней хватит лекарств, нужно определить, когда закончатся таблетки в пузырьке.
Мы будем повторять цикл из a дней до тех пор, пока в пузырьке останутся таблетки. В каждый из этих дней Белла будет принимать b таблеток, а Аполлинария будет принимать 1 таблетку один раз в a дней.
Например, для условий задачи (2, 3, 12):
1-й день: Белла -3, Аполлинария -1, осталось 8.
2-й день: Белла -3, Аполлинария 0, осталось 5.
3-й день: Белла -3, Аполлинария -1, осталось 1.
4-й день: Белла -3, нет достаточного количества таблеток.
Поэтому, при данных условиях таблеток хватит на 3 дня.
3. Мастерство фотографии
Фотографа попросили сделать фотосессию группы детей для выпускного альбома в детском саду. В числе прочих, он должен сделать групповой снимок, на котором должны присутствовать все дети одновременно. Фотограф считает, что для красивой фотографии группы требуется очень тщательно расставить детей в кадре. В частности, с его точки зрения, группа должна расположиться как можно компактнее по ширине, то есть количество людей в самом длинном ряду на фотографии должно быть как можно меньше.
Для гармоничного расположения детей фотограф размещает детей не более чем в четыре ряда. Девочек он располагает либо во втором ряду, сидящими на стульчиках, либо стоящими третьем ряду. Мальчиков он размещает либо в первом ряду, сидящими на корточках, либо в четвёртом ряду, стоящими на стульчиках. Группа состоит из a
мальчиков и b девочек. В студии есть стулья в количестве c штук. Какие‑то ряды могут быть пустыми. Все стулья использовать не обязательно.По заданным числам a, b и c требуется определить, какого наименьшего по ширине расположения группы сможет добиться фотограф.
Замечание
Во всех примерах в условии группа состоит из 9 мальчиков и 15 девочек.
В первом примере стульев нет, поэтому все девочки стоят, все мальчики сидят на корточках, общая ширина группы 15.
Во втором примере есть 4 стула. Можно посадить 4 девочек во втором ряду на эти стулья, остальные 11 девочек будут стоять в третьем ряду. Все мальчики будут сидеть на корточках в первом ряду. Общая ширина группы 11.
В третьем примере есть 7 стульев. Тогда есть два способа получить группу ширины 9. Например, можно посадить на все стулья девочек, тогда в первом ряду будет 9
мальчиков, во втором ряду будет 7 девочек, в третьем ряду 8 девочек. Либо можно посадить на стулья 6 девочек и поставить одного мальчика в четвёртый ряд. Тогда получим 8 мальчиков в первом ряду, 6 девочек во втором, 9 девочек в третьем и 1
мальчика в четвёртом. В любом из этих двух случаев ширина группы равна 9.
В четвёртом примере стульев много и есть несколько способов организовать группу ширины 8. Один из способов такой: посадим на корточки 4 мальчика в первом ряду, далее посадим 8 девочек на стулья во втором ряду, оставшиеся 7 девочек встанут в третьем и 5 мальчиков поставим на стульчики в четвёртом.
Ввод — 9, 15, 0, 9, 15, 4, 9, 15, 7, 9, 15, 100
Вывод — 15, 11, 9, 8
4. Места в ряду
В зале есть ряд из n мест, пронумерованных числами от 1 до n слева направо. Пройти к любому месту можно либо с левого конца ряда, либо с правого. Первоначально некоторые места уже заняты и ещё k человек по одному садятся на свободные места. Каждый человек выбирает себе свободное место, до которого ближе всего идти от одного из концов ряда. Если же есть два свободных места, одинаково удалённых от левого и правого концов ряда, то человек выберет левое место (с меньшим номером).
Определите номера мест, которые будут выбирать люди, в порядке их прихода.
Первая строка входных данных содержит целое число n (1≤n≤2⋅10^5) — количество мест в ряду.
Вторая строка содержит целое число k (1≤k≤n) — количество приходящих людей.
Третья строка содержит строку s длины n, состоящую из символов «0» и «1» и задающую первоначальную рассадку. Занятые места обозначаются единицами, пустые — нулями. Гарантируется, что в строке s содержится не менее k нулей.
В первом примере первоначально заняты места 11, 22 и 66 (рисунок А).
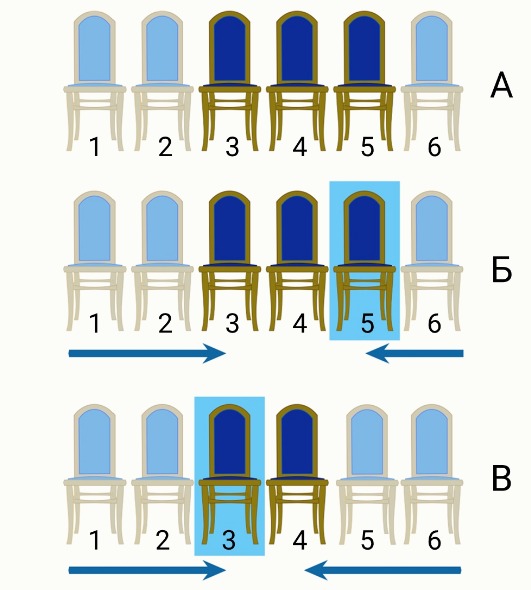
Если первый пришедший будет двигаться с левой стороны ряда, он пройдёт мимо 1 и 2
места, прежде чем доберётся до свободного места с номером 3. Если же он будет двигаться с правой стороны ряда, то ему понадобится пройти мимо одного места с номером 6, после чего он сможет занять место 5. Именно это место он и выберет (рисунок Б). Второй пришедший может занять либо место с номером 3, двигаясь с левой стороны и проходя мимо двух занятых мест 1 и 2, либо место с номером 4, двигаясь с правой стороны и проходя мимо двух занятых мест 6 и 5. Поскольку в обоих случаях ему нужно пройти мимо двух занятых мест, он будет двигаться с левой стороны и займёт место с номером 3.
Во втором примере в ряду 6 мест, второе и пятое места изначально уже заняты, заходят ещё 3 человека. Первый заходящий человек будет выбирать между первым и шестым местами, заходя с левого или правого края соответственно. В обоих случаях ему придётся пройти мимо нуля занятых мест, поэтому он решит зайти слева и сесть на 1 место. Второй человек будет выбирать между третьим и шестым местами. В первом случае ему придётся идти мимо двух занятых мест, во втором — мимо нуля, поэтому он выберет зайти справа — 6 место. Третий человек будет выбирать между третьим и четвертым местами. В обоих случаях ему придётся пройти мимо двух занятых мест, поэтому он выберет зайти слева — 3 место.
Ввод
6
2
110001
6
3
010010
Вывод
5 3
1 6 3
5. Гармония
Совсем недавно Васе на день рождения подарили строку, состоящую только из символов «0» и «1». Обрадованный этим подарком, он тут же начал эту строку изучать — искать в ней гармоничные части. Для начала Васю интересует только количество различных непустых гармоничных подстрок. А поскольку подарок оказался слишком большим, мальчик решил обратиться за помощью к вам. Помогите Васе!
В понимании Васи, строка является гармоничной, если и символов 0, и символов 1 в ней чётное количество. Подстрокой строки s называется строка, полученная из s выкидыванием нескольких символов с начала и с конца (возможно, нуля или всех). Так, строка «12» является подстрокой строки «123», а строка «13» — нет. Подстроки считаются одинаковыми, если у них совпадает количество удалённых символов с начала и с конца.
Замечание
В первом примере из условия подходят следующие подстроки (выделены жирным): 001100, 001100, 001100, 001100, 001100, 001100, 001100.
Ввод
6
001100
1
0
Вывод
7
Решение:
По определению Васи, «гармоничная» подстрока – это та, в которой количество символов «0» и «1» четное. Для подсчета всех гармоничных подстрок необходимо проанализировать все возможные подстроки этой строки.
У нас есть строка «001100», длиной 6 символов. Её подстроками могут быть:
«0», «00», «001», «0011», «00110», «001100» (символы с левого края)
«0», «01», «011», «0110», «01100» (если выкинуть 1 символ слева)
«1», «10», «100», «1001» (если выкинуть 2 символа слева)
«0», «00», «001» (если выкинуть 3 символа слева)
«0», «01» (если выкинуть 4 символа слева)
«1» (если выкинуть 5 символов слева)
Из всех этих подстрок гармоничными будут:
«00», «0011», «001100», «01», «10», «0011», «0110», что в сумме получается 7 гармоничных подстрок.
Ответы появятся по мере их решения!
