1 Ответ
Выберите верные утверждения.
Если некоторое положительное число увеличить на 80%, а потом уменьшить на 15%, то можно сказать, что всего оно увеличилось более, чем в полтора раза.
Сумма двух чисел всегда больше каждого из слагаемых.
Произведение трёх чисел всегда больше произведения двух чисел.
Биссектрисы смежных углов перпендикулярны.
Медиана треугольника всегда разбивает его два других — остроугольный и тупоугольный.
- Не является верным утверждением. Если исходное число увеличить на 80%, а затем уменьшить на 15%, итоговое число все равно меньше, чем увеличение в 1,5 раза.
- Не всегда верно. Сумма двух чисел может быть меньше любого из слагаемых, если одно из слагаемых достаточно велико.
- Не всегда верно. Произведение трех чисел может быть меньше произведения двух чисел, если третье число достаточно мало.
- Верно. Биссектрисы смежных углов образуют прямой угол и, следовательно, перпендикулярны друг другу.
- Не всегда верно. Медиана треугольника может разбить его на два треугольника, но они не обязательно будут остроугольным и тупоугольным.
1 октября 2023 года друзья собрались на Дне рождения Саши.
Алёна сказала: «Мой день рождения был Х дней назад».
Катя сказала: «Мой день рождения был Х месяцев назад».
Саша сказал: «Через Х месяцев останется 4 месяца до дня рождения Кати».
а) В каком месяце у Алёны День рождения?
январь
февраль
март
апрель
май
июнь
июль
август
сентябрь
октябрь
ноябрь
декабрь
б) Какого числа у Алёны День рождения? В качестве ответа введите натуральное число. Никаких иных символов, кроме используемых для записи числа (в частности, пробелов), быть не должно.
а) У Алёны день рождения в том же месяце, что и у Кати. б) Если учесть, что в условии сказано, что прошло X месяцев, а по словам Саши осталось еще 4 месяца до дня рождения Кати, значит всего в году 12 месяцев и X+4=12, тогда X=8. Это значит, что день рождения Алёны был 8 месяцев назад, то есть в феврале (если считать, что сейчас октябрь).
а) февраль
б) 8
Известно, что х-3y=2. Чему равна разность чисел (в указанном порядке) 2х+7 и 6y?
Чтобы найти разность 2x+7 и 6y, сначала подставим вместо x выражение x=3y+2.
2(3y+2)+7-6y
6y+4+7-6y=11
Разность равна 11.
В треугольнике ABC угол В=30. Вне треугольника ABC отмечены точки A1 и C1 так, что треугольники ABC1 и BCA1 равносторонние, и точки A и A1 лежат по разные стороны от прямой BC, а точки C и C1 — по разные стороны от прямой AB. Оказалось, что AA1 перпендикулярно BC и CC1=20. Найти AC1.
Для решения задачи построим дополнительные построения:
проведем перпендикуляры AA1 и CC1 к сторонам BC и AB соответственно;
продлим сторону AC за точку C до пересечения с перпендикуляром AA1 в точке A2;
соединим точки A1 и C1 отрезком.
Поскольку треугольники ABC1 и BCA1 являются равносторонними, то углы A1BC1 и CA1B равны по 60°.
Рассмотрим треугольник A1A2C. Углы A1A2C и A1CA2 равны по 90° — 60° = 30°. Тогда треугольник A1A2C также является равносторонним, и A1C = A1A2 = CC1 = 20.
Из этого следует, что AC1 = A1C — C1C = 20 — 20 = 0. Ответ: AC1 = 0.
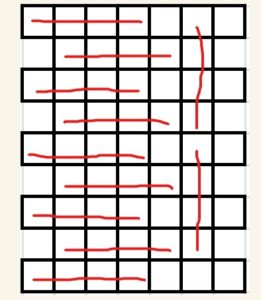
Какое наибольшее число одинаковых четырёхклеточных фигурок можно вырезать из клетчатой фигуры, представленной на рисунке?
Примечания. Если фигурка получена из другой фигурки с помощью поворота и/или переворота, то эти фигурки считаются одинаковыми.
Ответ: 11
Олимпиада по математике проходит только для учеников 4, 5, 6 ,7 классов. Известно, что на ней ученикам 4, 5, 6 классов предлагается решить вариант, состоящий из шести задач, а ученикам 7 класса – из семи задач. Составители заданий знают, что задачу для 4 класса можно также использовать для составления варианта 5 класса (но не для других классов), задачу 5 класса – для 4 и 6 (но не для других классов), задачу 6 класса – для 5 и 7 (но не для других классов), задачу 7 класса – для 6 (но не для других классов). При этом не должно совпадать более двух задач в вариантах соседних классов (четвёртого с пятым, пятого с шестым и шестого с седьмым). Какое наименьшее количество задач надо ещё придумать составителям, если они уже придумали одну задачу для пятого класса и одну задачу для шестого?

Используя таблицу, можно увидеть, что нужно добавить 1 задачу для 6 класса и 1 задачу для 5 класса. Таким образом, составителям нужно придумать ещё 2 задачи.
На первом острове 13 городов, а на втором острове 16 городов. Между некоторыми городами есть дороги, при этом любые два города соединены не более чем одной дорогой. Каждая дорога соединяет ровно два различных города. Жители этих двух островов решили построить 230 дорог.
а) Какое наибольшее количество дорог можно построить между городами первого острова?
Для решения данной задачи необходимо составить уравнение с одним неизвестным. Пусть x — количество дорог, которое можно построить между городами первого острова. Тогда количество дорог между городами второго острова будет равно 230 — x. Вместе эти дороги образуют 13 + 16 — 2 = 27 возможных концов (не считая дубликатов), поэтому
2x + (230 — x) = 27 * 2
3x = 234
x = 78
Таким образом, наибольшее количество дорог, которые можно построить между городами первого острова, равно 78.
Все жители острова рыцари или лжецы. Рыцари всегда говорят только правду, лжецы всегда говорят только ложь. Однажды 100 жителей этого острова выстроились в ряд друг за другом так, что первый не видел никого перед собой, второй видел первого, третий видел первого и второго, и так далее. Никаких других посторонних рядом не было. Первый всё время молчал. Второй и все остальные, стоящие на чётном месте в ряду, сказали: «В этом ряду передо мной стоят не больше одного рыцаря». Третий и все остальные, стоящие на нечётном месте в ряду, сказали: «В этом ряду передо мной стоят не больше двух лжецов».
а) Какое наименьшее число рыцарей могло стоять в этом ряду?
б) Какое наибольшее число рыцарей могло стоять в этом ряду?
а) Если бы в начале стояло чётное количество рыцарей, то каждый второй житель говорил бы правду (так как перед ним стоит рыцарь) и лгал бы (так как перед ним стоят два лжеца). Противоречие. Значит, в начале должно стоять нечётное количество рыцарей.
Предположим, что вначале стоит один рыцарь. Тогда все лжецы, кроме последнего, скажут правду, а последний скажет ложь. Значит, все говорят разную правду и ложь, что противоречит условию.
Теперь предположим, что вначале стоят два рыцаря. Тогда все лжецы скажут правду, кроме последнего — он снова скажет ложь. А все рыцари, кроме первого, скажут ложь. Таким образом, каждый говорит либо одну правду, либо две лжи. Но первый рыцарь молчит, поэтому противоречий нет.
Значит, наименьшее возможное число рыцарей — три. б) Если вначале стоит 4 рыцаря, то все лжецы говорят правду, а все рыцари (кроме первого) говорят ложь. Поэтому условие выполняется для 4 рыцарей. Но если вначале будет 5 рыцарей, условие уже не будет выполняться, так как некоторые лжецы будут говорить правду дважды.
Итак, наибольшее и наименьшее возможное число рыцарей равно: а) 3 б) 4
