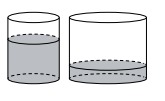
В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.
1 Ответ
Объем жидкости в первом сосуде равен объему жидкости во втором сосуде, так как объем цилиндра пропорционален квадрату радиуса основания и не зависит от высоты.
Таким образом, объем жидкости во втором сосуде можно найти, умножив объем первого сосуда на 4, так как радиус основания второго сосуда в 2 раза больше радиуса основания первого сосуда.
Объем первого сосуда равен π * r^2 * h, где r — радиус основания, h — высота уровня жидкости.
Так как радиус основания первого сосуда r = 2h, то объем первого сосуда можно выразить как π * (2h)^2 * 16 = 64π * h^2.
Тогда объем второго сосуда будет равен 64π * 4 * h^2 = 512π * h^2, так как диаметр основания второго сосуда равен 2 * диаметр первого сосуда, а радиус основания равен половине диаметра.
Найдем высоту уровня жидкости во втором сосуде:
h = 4
Ответ: уровень жидкости во втором цилиндрическом сосуде будет находиться на высоте 4 см.
