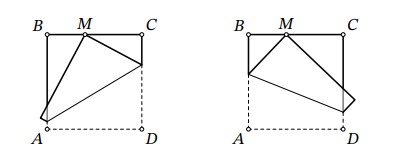
У Лёши есть бумажный квадрат ABCD. Он отметил на стороне BC точку M. Сначала он перегнул квадрат так, что точка D совпала с точкой M (левый рисунок), и разогнул обратно. Затем он перегнул его так, что точка A
совпала с точкой M (правый рисунок), и снова разогнул обратно. Пусть O — точка пересечения двух линий перегиба. Докажите, что BO = OC.
1 Ответ
Решение.
Заметим, что при первом перегибании отрезок DO совмещается с MO, а при втором — отрезок AO совмещается с MO. Следовательно, AO = MO = DO (рис. 1).
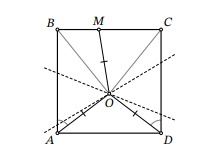
Получаем, что треугольник AOD равнобедренный. Теперь докажем, что треугольники AOB и DOC равны по первому признаку. Действительно:
AB = CD, так как это две стороны квадрата
AO = OD из-за того, что AOD равнобедренный
∠BAO = 90◦ − ∠OAD = 90◦ − ∠ODA = ∠CDO
Тогда BO = OC, что и требовалось доказать
