У Пети есть 2023 камня, массы любых двух из которых различаются не более чем в 2 раза. Докажите, что Петя может разложить все камни по кучам так, чтобы в каждой куче было ровно 7 камней?

Решение.
Разложим камни в ряд по возрастанию масс слева направо и разобьём их на последовательные семёрки. Эти семёрки сделаем кучами. Докажем, что среди них будет не более 7 странных. Назовём показателем каждой семёрки массу правого камня в ней. Заметим, что у странной семёрки (т. е. образующей странную кучу) показатель более чем на 10% больше, чем у семёрки слева от неё. (Если самая левая семёрка образует странную кучу, то слева от неё поместим виртуальную семёрку без камней,
показателем которой сделаем массу самого лёгкого камня ряда. Тогда утверждение будет корректным для всех странных семёрок.)
Предположим, что в ряду оказалось хотя бы 8 странных семёрок. Это означает, что, если идти по ряду слева направо, показатель будет не менее 8 раз увеличиваться более чем на 10% (а в остальных случаях не убывать). Оценим наименьшее возможное значение показателя по сравнению с его изначальной величиной. Каждую операцию увеличения на 10% обозначим стрелкой «7→»; та как нам нужно оценить наименьший возможный результат, будем округлять числа до сотых в меньшую сторону:

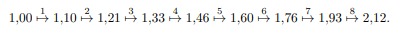
Так как все показатели — это массы каких-то камней в ряду (в том числе показатель виртуальной семёрки, которую мы могли добавить), то они не могут увеличиться более чем в два раза. Противоречие. Значит, в ряду получилось не более 7 странных семёрок.