Тимофею на день рождения родители подарили металлоискатель. Естественно, наутро мальчик отправился на поиски клада. Он предположил, что когда‑то давно кто‑то мог обронить золотую монету на древней прямой дороге, и для облегчения поиска придумал систему координат. Ось абсцисс OX направлена вдоль дороги, а ось ординат OY направлена вверх.
Устройство работает следующим образом: на его индикаторе выставляется натуральное число r, и если ровно на этом расстоянии имеется золотой предмет, то загорается зелёная лампочка.
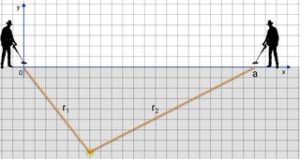
Сначала юный кладоискатель выставил число r1 в точке x=0, затем отошёл в точку с абсциссой x=a и выставил число r2, как показано на рисунке. Новичкам везёт, оба раза загорелась зелёная лампочка.
Определите координаты потерянной когда‑то давно золотой монетки.
1 Ответ
Для решения этой задачи можно использовать знания из алгебры и геометрии.
1. Определить координаты точки, в которой находится металлоискатель. Пусть это будет точка (x, y), где x — координата по оси OX, а y — координата по оси OY.
2. Определить диапазон поиска. Пусть это будут координаты (a, b), где a и b — координаты точек, в которых металлоискатель может находиться в процессе поиска.
3. Определить границы области поиска. Пусть она будет ограничена прямоугольником с вершинами в точках (-a, -b), (-a, b), (a, b) и (a, -b).
4. Найти все точки внутри области поиска, которые удовлетворяют условию металлоискателя. Для этого можно использовать формулу металлоискателя:
Расстояние от точки 0 до a — это гипотенуза треугольника, а r и r2 — его катеты.
Тогда положение монетки на оси y — это высота треугольника, которая находится по формуле h = 2* sqrt(p(p — a)(p — b)(p — c)) / a, где p — периметр треугольника (а + b + c).
А положение монетки на оси x — расстояние от 0 до h, которое найдешь по теореме Пифагора — один катет (h) и гипотенуза (точка 0 — монетка)
отсюда находишь второй катет
sqrt(r(1)**2-h**2))
