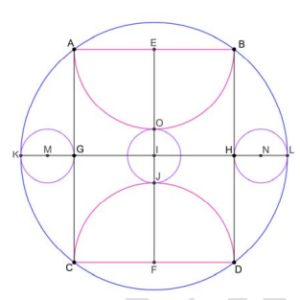
В окружность ω вписан прямоугольник ACDB. На отрезках AB и CD как на диаметрах внутри прямоугольника ABCD построены полуокружности Ω₁ и Ω₂ соответственно. Окружность ω₁ с центром в точке M внутренним образом касается окружности ω в точке K и касается отрезка AC в точке G. Окружность ω₂ с центром в точке I внешним образом касается полуокружностей Ω₁ и Ω₂ в точках O и J соответственно. Окружность ω₃ с центром в точке N внутренним образом касается окружности ω в точке L и касается отрезка BD в точке H (см. рис.). Пусть S, S₁, S₂, S₃ – площади кругов, ограниченных окружностями ω, ω₁, ω₂, ω₃ соответственно. Пусть также S₄ – площадь полукруга, ограниченного полуокружностью Ω₁ и отрезком AB. И пусть S₅ – площадь полукруга, ограниченного полуокружностью Ω₂ и отрезком CD . Найдите значение выражения (S₁+S₂+S₃+S₄+S₅)/S.