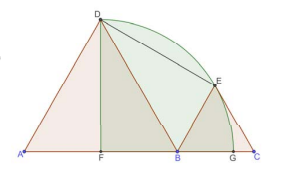
Даны два равносторонних треугольника ABD и BCE. Построена четверть окружности FGED с центром F и радиусом FD=FE=FG. Точки A, F, B, G и C лежат на одной прямой (см. рис.). Найдите длину отрезка DE, если известно, что площадь сектора круга FGED равна 9π.
Arnfinn ответил на вопрос
1 Ответ
Решение:
Пусть BD = x, DE = y, FD = z. Тогда FGED — окружность, центр которой лежит на прямой BC, а радиус равен FG = AB / 2 = x / 2. Если мы соединим точки A, D и F, то получим треугольник ADF, который равнобедренный и не содержит точку D. Точка D лежит на окружности FG, и её радиус FG = FD/2. Следовательно, FGED — окружность. Точки E и G — центры окружностей FGED и FDG, поэтому FGED = FDG = FG × FG / 4 = FG / 4. Отсюда находим, что FG = ^2FG / 4 × FD × DE. Тогда DE = FG — FG / 2 × FD
Arnfinn ответил на вопрос
