1 Ответ
1. Острый угол 𝐵 прямоугольного треугольника равен 66°. Найдите угол между биссектрисой 𝐶𝐷 и медианой 𝐶𝑀, проведёнными из вершины прямого угла. Ответ дайте в градусах.
Ответ: 21
2. Длины векторов 𝑎⃗ и 𝑏⃗⃗ равны 3 и 5, а угол между ними равен 60°. Найдите скалярное произведение 𝑎⃗ ∙ 𝑏⃗⃗.
Ответ: 7,5
3. Найдите объём многогранника, вершинами которого являются точки A, D, А1, В, С, В1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 4, AA1= 5.
Ответ: 30
4. Научная конференция проводится в 4 дня. Всего запланировано 80 докладов – первые два дня по 12 докладов, остальные распределены поровну между третьим и четвёртым днями. На конференции планируется доклад профессора М. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Ответ: 0,35
5. Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Ответ: 0,6
6. Найдите корень уравнения 6^1+3𝑥=36^2𝑥.
Ответ: 1
7. Найдите значение выражения log52/log513+log130,5
Ответ: 0
8. На рисунке изображён график функции у = f(x) — производной функции f(x), определённой на интервале (-3;8). Найдите точку максимума функции f (x).
Ответ: 7
9. Для обогрева помещения, температура в котором поддерживается на уровне 𝑇п=25°С, через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды 𝑚=0,3 кг/с. Проходя по трубе расстояние 𝑥, вода охлаждается от начальной температуры…коэффициент теплообмена, а 𝛼=1,4 — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 56 м.
Ответ: 33
10. Имеется два сосуда. Первый содержит 80 кг, а второй – 70 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 63% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 65% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Ответ: 28
11. На рисунке изображён график функции вида 𝑓(𝑥)=log𝑎𝑥. Найдите значение 𝑓(16)
Ответ: -4
12. Найдите наименьшее значение функции у = (2x + 15) • e2x+16 на отрезке [-12; — 2].
Ответ: -1
13. Решите уравнение:
а) log13(cos 2x-9VZcosx-8) = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку [−2𝜋;−𝜋/2].
Ответ:
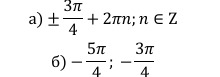
14. В треугольной пирамиде SABC известны боковые рёбра: SA = SB = 13, SC = 3117. Основанием высоты этой пирамиды является середина медианы СМ треугольника АВС. Эта высота равна 12.
а) Докажите, что треугольник ABC равнобедренный.
б) Найдите объём пирамиды SABC.
Ответ: 96
15. Решите неравенство: logo,5 (x3 — 3×2 — 9x + 27) < log0,25(x — 3)4.
Ответ: [−2;3) ∪ (3;+∞)
16. В июле 2020 года планируется взять кредит в банке на некоторую сумму.
Условия его возврата таковы: – каждый январь долг увеличивается на 𝑟% по сравнению с концом
предыдущего года; – с февраля по июнь каждого года необходимо выплачивать одним платежом
часть долга. Если ежегодно выплачивать по 1 464 100 рублей, то кредит будет полностью
погашен за 4 года, а если ежегодно выплачивать по 2 674 100 рублей, то кредит будет полностью погашен за 2 года. Найдите 𝑟.
Ответ: 10
17. В трапеции ABCD угол BAD прямой. Окружность, построенная на большем основании AD как на диаметре, пересекает меньшее основание ВС в точках С и М.
а) Докажите, что ZBAM = LCAD.
б) Диагонали трапеции ABCD пересекаются в точке О. Найдите площадь треугольника АОВ, если AB = V10, а ВС = 2ВМ.
Ответ: 3√2
18. Найдите все значения а, при каждом из которых уравнение x2 + (a + 7)} = \x — 7 — a| +|x + a + 7| имеет единственный корень.
Ответ: {−5} ∪{−9}
19. На доске написано 𝑛 единиц подряд. Между некоторыми из них расставляют знаки «+» и считают получившуюся сумму. Например, если было написано 10 единиц, то можно получить сумму 136: 1+1+111+11+11+1=136
а) Можно ли получить сумму 141, если 𝑛=60? = да
б) Можно ли получить сумму 141, если 𝑛=80? = нет
в) Для скольких значений 𝑛 можно получить сумму 141? = 15
