1 Ответ
Задание 1. Боковые грани пирамиды четыре равных равнобедренных треугольника. На этих гранях проведены отрезки, параллельные основанию, как показано на чертеже. Длины путей, отмеченные на чертежах красным, соответственно равны a, b и c.
Выберите верное утверждение:
c>b=a
b=c>a
a=b=c
a<b<c +
Задание 2: Действительные числа x и y таковы, что:
9х/у=ху=2х+4у
Какое наибольшее значение может принимать y? = 12
Задание 3: На чертеже четырёхугольник ABCD вписан в окружность ω. Прямая, проходящая через точку D и параллельная AB, пересекает ω в точке P. Известно, что ∠PDC=20∘, ∠DPB=85∘.
Найдите величину угла ∠ABC. Ответ выразите в градусах. = 115
Задание 4: Натуральные числа a, b и c таковы, что НОД (a, b) =2 и НОД (b, c) =4.
Чему может быть равен НОД (a, c)? Выберите все верные ответы:
1
2 +
3
6 +
12
Задание 5: У Жоры есть коробка конфет, в которой конфеты расположены прямоугольником 4×10 (4 строчки, 10 столбцов). Жора берёт по одной конфете, каждый раз выбирая из строки, в которой осталось максимальное количество конфет; если таких несколько из любой из них. Сколькими способами Жора мог съесть первые 5 конфет? Порядок поедания важен. = 8640000
Задание 6: Прямая ℓ, пересекающая стороны AB и AC треугольника ABC, разбивает его на равносторонний треугольник и на четырёхугольник. Пусть X и Y проекции точек B и C на прямую ℓ. Найдите длину отрезка XY, если AB=19, AC=24. Ответ: 21,5
Задание 7: В стране 3 мегаполиса и 6 городков. Авиакомпания планирует расписание полётов между ними. Руководитель хочет, чтобы выполнялись следующие условия:
от любого населённого пункта до любого другого можно добраться (прямым рейсом или с пересадками);
если из пункта A есть рейс в пункт B, то и из пункта B есть рейс в пункт A;
из двух мегаполисов можно улететь ровно в три населённых пункта, а из одного в четыре;
из каждого городка можно улететь ровно в один населённый пункт.
Сколько существует способов организовать такое расписание? = 180
Задание 8: Числа a1, a2, ……, a9 таковы, что: Какое наибольшее значение может принимать a1?
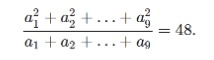
Ответ: 48
