Сколько Степе потребуется перестановок, чтобы закончить игру при исходной последовательности бочонков 52314?

1.Пирамида

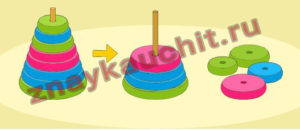
Андрей играет с пирамидой, составленной из колец, по своему алгоритму.
В результате из левой пирамиды получилась правая, в которой на четыре кольца меньше.
Каким алгоритмом воспользовался Андрей при снятии колец с пирамидки?
А. Ни один из указанных
Б. ПОВТОРЯТЬ: ЕСЛИ верхнее кольцо НЕ красное, ТО снять кольцо
В. ЕСЛИ верхнее кольцо красное, ТО снять кольцо
Г. ПОВТОРЯТЬ: ЕСЛИ верхнее кольцо красное, ТО снять кольцо
Д. ЕСЛИ верхнее кольцо НЕ красное, ТО снять кольцо

2. Перекличка.

Бобры Ваня, Слава, Антон, Борис, Егор и Петя, стоящие именно в таком порядке, решили поиграть в перекличку.
Бобры выстраиваются в ряд и начинают выкрикивать свои имена: первый бобер называет свое имя; второй бобер называет имя первого, а потом свое; третий бобер называет имя первого и второго, а потом свое, и так далее.
Какое имя будет названо пятнадцатым по счету?
А. Петя
Б. Антон
В. Слава
Г. Ваня
Д. Егор
Е. Борис

Давайте, чтобы было более понятно и не прибегать к решениям, просто посчитаем с помощью такой таблицы:
1. Ваня.
2. Ваня, Слава
3. Ваня, Слава, Антон
4. Ваня, Слава, Антон, Борис
5. Ваня, Слава, Антон, Борис, Егор
6. Ваня, Слава, Антон, Борис, Егор, Петя.
Теперь считаем: Ваня, Ваня, Слава, Ваня, Слава, Антон, Ваня, Слава, Антон, Борис, Ваня, Слава, Антон, Борис, Егор = 15. Значит 15 по счету будет звучать имя — Егор.

3. Размен.

У Васи есть много монет по 1 рублю, по 2 рубля и по 5 рублей.
Какую наименьшую сумму в рублях он НЕ сможет набрать, использовав одну, две или три монеты?

Давайте посчитаем: Вася может использовать от 1 до трех монет, скорее всего любого номинала (1, 2 и 5). Если он возьмет по одной монете с каждого числа, значит он может собрать суму в 1 рубль, 2 рубля или 5 рублей. Если он возьмет по две монеты, значит он может собрать сумму: 2 (1+1), 4 (2+2), 3 (2+1), 6 (5+1), 7 (2+5), 10 (5+5).  Если он возьмет три монеты, то получит суммы: 3 (1+1+1), 6 (2+2+2), 15 (5+5+5), 8 (1+2+5), 11 (1+5+5), 12 (2+5+5), 9 (2+2+5). И того, из монет он получить суммы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 15. А суммы в 13 и 14 Вася получить не сможет.

4. Взгляд со стороны

Все грани кубика покрашены в разные цвета.
Четыре мальчика посмотрели на кубик снаружи с разных сторон, и каждый нарисовал то, что увидел. Три мальчика нарисовали свою картинку правильно.
Какая картинка ошибочна?
А. Б. В. Г.

5. Матрёшки

У восьми матрешек есть несколько признаков, по которым они различаются:
Цвет платка на голове
Цвет сарафана
Цвет цветочка на сарафане
Цвет рукавов рубашки под сарафаном
Цвет основания, на котором стоит матрешка.

Здесь, можно заметить, что матрешки имеют:
1. Голубые и желтые платки на голове
2. Красные и зеленые сарафаны
3. Розовые и коричневые подставки
4. Желтые и розовые цветы на сарафане
И только одно отличие есть у одной матрешки (первая), розовые рукава рубашки. У остальных матрешек они зеленые.

6. Пиксели

В компьютере растровые картинки хранятся в виде последовательности чисел, описывающих цвет пикселей — маленьких квадратиков. Если картинка двухцветная, то шифрование пикселей картинки осуществляется числами 0 и 1 слева направо и сверху вниз. 0 или 1 — это один бит информации. 8 бит образуют один байт.
Какая картинка 16☓9 зашифрована следующей последовательностью байтов?

00000111 11100000 00000100 00100000 00000100 00100000 00000100 00100000 00000100 00100000 00000100 00100000 00000100 00100000 00000100 00100000 00000100 00100000

Ответ: Это картинка — А

7. Сортировка лото

Бобёр Степа играет в лото. Он наугад выкладывает перед собой в ряд пять бочонков с номерами от 1 до 5.
Далее, двигаясь от начала ряда к концу, последовательно сравнивает числа на соседних бочонках. Если предыдущее число оказывается больше последующего, он меняет их местами (совершает перестановку). То есть сначала он сравнивает первый со вторым, потом второй (он мог поменяться с прошлого шага) с третьим, и так далее. Дойдя до конца ряда, Степа возвращается к первому бочонку и продолжает действовать таким же образом до тех пор, пока бочонки не встанут в ряд от 1 до 5.
Сколько Степе потребуется перестановок, чтобы закончить игру при исходной последовательности бочонков 52314?

Итак, у нас дана исходная последовательность бочонков: 52314.
Степа начинает сравнение чисел на соседних бочонках и производит перестановки, если предыдущий бочонок больше следующего.
1. Сначала сравниваем 5 и 2. Поскольку 5 > 2, меняем их местами. Получаем последовательность 25314.
2. Затем сравниваем 5 и 3. Поскольку 5 > 3, меняем их местами. Получаем последовательность 23514.
3. Потом сравниваем 5 и 1. Поскольку 5 > 1, меняем их местами. Получаем последовательность 21534.
4. Теперь сравниваем 2 и 1. Поскольку 2 > 1, меняем их местами. Получаем последовательность 12534.
5. Сравниваем 5 и 3. Поскольку 5 > 3, меняем их местами. Получаем последовательность 12354.
6. Сравниваем 5 и 4. Поскольку 5 > 4, меняем их местами. Получаем последовательность 12345.
Теперь все бочонки стоят в ряд от 1 до 5, и Степа завершает игру.
Итого, Степе потребовалось 6 перестановок, чтобы закончить игру при исходной последовательности бочонков.

8. Бинарные коды

Рассмотрим все двоичные коды цифр длины три:
“0” — 000, “1” — 001, “2” — 010, “3” — 011, “4” — 100, “5” — 101, “6” — 110, “7” — 111.
Расставьте цифры от 0 до 7 так, чтобы коды соседних цифр отличались в одном разряде.
Например “2” и “3” можно поставить рядом, так как они отличаются только в последнем двоичном разряде, а “3” и “4” нельзя, так как различия у них во всех трех разрядах.
Первой стоит цифра “0”. Поставьте остальные.

В начале условия задачи приведены двоичные коды цифр от 0 до 7. Найдем двоичную запись каждой цифры и проанализируем, в каких разрядах они отличаются друг от друга соседними числами.
0 — 000
1 — 001
2 — 010
3 — 011
4 — 100
5 — 101
6 — 110
7 — 111
Изначально в задаче указано, что первой цифрой должна быть «0». Следовательно, первая цифра уже определена, и её расположение не требуется изменять.
Теперь, приступим к остальным цифрам. Рассмотрим номера разрядов.
Разряд 1:
0 — 0
1 — 0
2 — 0
3 — 0
4 — 1
5 — 1
6 — 1
7 — 1
Из этих данных видно, что первая цифра нашей последовательности — «0».
Разряд 2:
0 — 0
1 — 0
2 — 1
3 — 1
4 — 0
5 — 0
6 — 1
7 — 1
Из этих данных видно, что вторая цифра нашей последовательности — «4».
Разряд 3:
0 — 0
1 — 1
2 — 0
3 — 1
4 — 0
5 — 1
6 — 0
7 — 1
Из этих данных видно, что третья цифра нашей последовательности — «2».
Таким образом, для того чтобы равномерно расставить цифры от 0 до 7 так, чтобы различия между кодами в соседних разрядах были минимальными, мы получаем следующую последовательность:
0 — 000
4 — 100
2 — 010
6 — 110
1 — 001
5 — 101
3 — 011
7 — 111
Таким образом, последовательность будет выглядеть следующим образом:
0, 4, 2, 6, 1, 5, 3, 7.

9. Две улитки

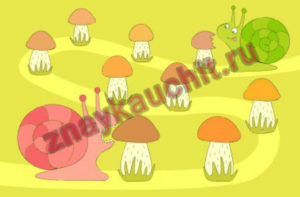
Старая Красная улитка ползет по дорожке и поедает грибы.
За минуту она съедает гриб, потом минуту она отдыхает, затем ещё минуту ползёт к следующему грибу. И так далее.
Молодая Зеленая улитка ползет ей навстречу.
Она также за минуту съедает гриб, а потом (не отдыхая) минуту ползёт к следующему грибу.
Если гриб уже поедает одна улитка, то другая его не трогает и отдыхает?
За сколько минут улитки съедят все 9 грибов?

Так как в задачке не обозначено, сколько грибов съела каждая улитка, тогда можно предположить, что каждой улитке досталось по 4.5 гриба. (9 делим на 2). У красной улитки на каждый гриб уходит 3 минуты, значит 4.5 * 3 = 13.5 минут. У зеленой улитки на гриб уходит 2 минуты, значит 4.5 * 2 = 9 минут. Из этого: 13.5 + 9 = 22.5 минуты уходит обе улитки съедят 9 грибов.

10. Лестница Пенроуза

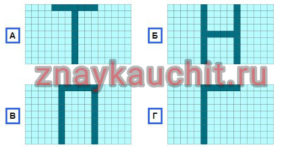
Алиса и Белый Кролик начинают подниматься по странной лестнице, изображённой на рисунке.
Она называется лестницей Пенроуза. У данной лестницы 45 ступенек.
Алиса за секунду прыгает через ступеньку, а Белый Кролик — через шесть.
Начинают они вместе.
Через сколько секунд Белый Кролик и Алиса вновь окажутся на одной ступеньке?

Ответ: Алиса и Кролик окажутся на одной ступеньке через 7 секунд. Если учитывать на какой ступеньке на картинке находиться Кролик.

11.Плитка

Пол у Васи в квартире состоит из 49 красных и белых плиток, уложенных как попало.
Вася хочет, чтобы от каждой красной плитки можно было добраться до любой другой красной, переходя каждый раз на соседнюю по горизонтали или вертикали красную плитку, и чтобы от каждой белой плитки можно было добраться до любой другой белой, переходя каждый раз на соседнюю по горизонтали или вертикали белую плитку.
Какое наименьшее число плиток он должен перекрасить?

12. Бедные слова

Будем говорить, что одно слово беднее другого, если другое слово содержит все его буквы. Например, слово МОЛОКО беднее слова МОЛЕКУЛА.
Назовём слово самым бедным в наборе, если там нет ни одного слова беднее его.
Самых бедных слов может быть несколько.
Сколько в наборе: КРАБ, БАРАН, КОРОНА, КОБУРА, НАБОР, БУРАН самых бедных слов?
А. 6
Б. 3
В. 2
Г. 1
Д. 4
Е. 5

В наборе (КРАБ, БАРАН, КОРОНА, КОБУРА, НАБОР, БУРАН) два самых бедных слова: КРАБ и БАРАН. Это можно проверить, составив различные комбинации букв в этих словах: ни одна из них не содержит все буквы другой.

13. Домино

Бобёр Вася выкинул из набора домино все костяшки с пустышками. После этого у него осталась 21 костяшка. Каждая костяшка состоит из двух половинок, на каждой половинке от 1 до 6 точек, при этом все костяшки различны. Вася попробовал выложить доминошки в ряд по следующему правилу: две костяшки прикладываются друг к другу одинаковыми половинками (см. рисунок).
Вскоре он понял, что выложить все костяшки в ряд у него не получится.
Какое наименьшее суммарное число точек может быть на оставшихся у Васи доминошках?

Здесь могут быть доминошки: 4:6, 6:4, 4:4, 4:2, 2:6, 6:1, 1:2, 2:1, 1:1. Таким образом, наименьшее доминошка, может быть 1:1.

14. Бобровые счёты

Профессор Бобров из Бобруйска проводит опыты с бобрами. Он учит их счету и уже научил считать до трёх. Больших успехов бобры не достигли.
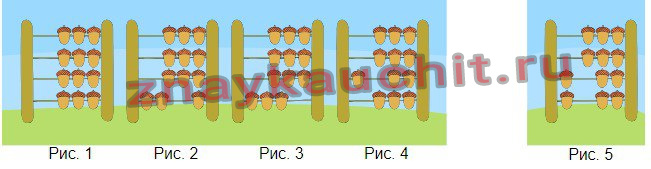
Поэтому для подсчета сваленных деревьев профессор Бобров сделал для них специальные счёты (рис. 1). На каждую палочку надето по 3 жёлудя.
Если надо, например, сложить 2+1, то бобры отодвигают на нижней палочке два жёлудя влево (рис. 2), потом отодвигают ещё один жёлудь влево, и, если получается 3 жёлудя (рис. 3), они возвращают их вправо, но на следующей палочке отодвигают один жёлудь влево (рис. 4). Жёлудь на второй палочке обозначает тройку.
Если нужно сложить 2+2, они разбивают второе число на две единицы: 2+1+1 и складывают по очереди. В этом случае на нижней палочке ещё один жёлудь будет сдвинут влево (Рис. 5).
Для остальных палочках действуют те же правила: если на какой-то палочке слева становится три жёлудя, они сдвигаются направо, а на палочке сверху от этой один жёлудь сдвигается налево.
Какое наибольшее число деревьев могли насчитать бобры на этих счетах, не нарушая правил, описанных в условии?

На каждой палочке счетов бобры могут иметь не более 3 желудей. Учитывая, что профессор Бобров научил бобров считать до трех, значит, на каждой палочке они могут иметь не более трех желудей, чтобы не нарушать правила. Таким образом, на каждой палочке бобры могут иметь по 3 желудя, а всего палочек 4. Следовательно, наибольшее число деревьев, которое они могут насчитать, равно 3 * 4 = 12.

15. 25 монеток

У бобра Миши есть 25 монеток, расположенных в виде квадрата 5☓5. Изначально они все повернуты «решкой» вверх.
За одно действие Вася может перевернуть несколько монет, выложенных в форме прямоугольника (несколько прямоугольников для примера показаны на первом рисунке).
Какое наименьшее количество действий ему понадобится, чтобы монетки лежали “в шахматном порядке”, то есть одним из этих двух способов:

1. «Решки» и «орлы» чередуются по каждой строке и столбцу.
2. Каждая строка и столбец начинается с «решки».

Чтобы решить эту задачу, Васе нужно выполнить следующие действия:
1. Перевернуть монетки в верхнем левом углу 2☓2, чтобы они были «в шахматном порядке».
2. Перевернуть средний столбец 5 монеток, чтобы они были «в шахматном порядке».
3. Перевернуть верхний правый угол 3☓3, чтобы они были «в шахматном порядке».
4. Перевернуть нижний правый угол 4☓4, чтобы они были «в шахматном порядке».

Таким образом, Васе понадобится 4 действия, чтобы монетки лежали «в шахматном порядке».