У 100 школьников есть стопка из 101 карточки, которые пронумерованы числами от 0 до 100. Первый школьник перемешивает стопку, затем берет сверху из получившейся стопки по одной карточке, и при каждом взятии карточки (в том числе при первом) записывает на доску среднее арифметическое чисел на всех взятых им на данный момент карточках. Так он записывает 100 чисел, а когда в стопке остаётся одна карточка, он возвращает карточки в стопку, и далее все то же самое, начиная с перемешивания стопки, проделывает второй школьник, потом третий, и т.д. Докажите, что среди выписанных на доске 10000 чисел найдутся два одинаковых.
1 Ответ
Решение.
На 1-м шаге у каждого из 100 человек было выписано одно из чисел множества A1 = {0, 1, 2, . . 100}.

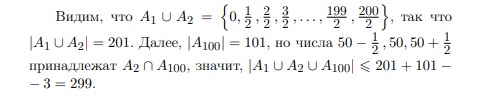
Итак, мы показали, что 300 чисел, выписанных на 1-м, 2-м и 100-м шагах, могут принимать не более 299 различных значений. Следовательно, какие-то два из них равны.
