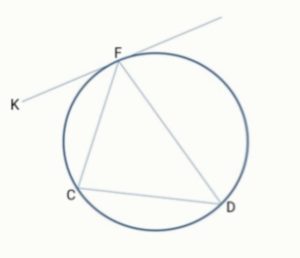
К описанной около треугольника FDC окружности проведена касательная FK, причём ∠KFC=66∘. Найти острый угол между биссектрисами углов CFD и FCD?

∠FDC = ∠KFC = 66˚

∠DFC + ∠DCF + ∠FDC = 180˚

∠DFC + ∠DCF = 180˚ — 66˚ = 114˚

Так как FB и CB — биссектрисы, то

∠BFC = ∠DFC/2 + ∠BCF = ∠DCF/2

Следовательно, ∠BFC + ∠BCF = (∠DFC + ∠DCF)/2 = 114˚/2 = 57˚

В таком случае, ∠FBC = 180˚ — (∠BFC + ∠BCF) = 180˚ — 57˚.

Учитывая, что ∠FBC и острый угол B — смежные углы и их сумма равна 180˚, соответственно,

острый ∠B = 180˚ — 180˚+ 57˚ = 57˚

Ответ: острый угол между биссектрисами  углов CFD и FCD равна 57˚.