1 Ответ
Задание 1. На конференцию по применению ИИ съехались 15 учёных из 15 разных стран, один из них — из России. У каждого
иностранного учёного есть совместные статьи ровно с 13-ю гостями конференции. Сколько участников конференции могут являться соавторами нашего соотечественника? Укажите все подходящие варианты. Каждый ответ записывайте в отдельное поле, добавляя их при необходимости.
Ответ: 0, 2, 4, 6, 8, 10, 12, 14
Задание 2. Ошибающийся чат-бот
Модель ИИ по запросу «Какое наибольшее число прямоугольников из 4 клеток можно вырезать из квадрата 25×25?» выдала ответ на запрос «Какое наибольшее число квадратиков из 4 клеток можно вырезать из прямоугольника 25 ×25?». На сколько ответ модели отличается от верного?
Ответ: 12
Задание 3. Решающее дерево глубины 2
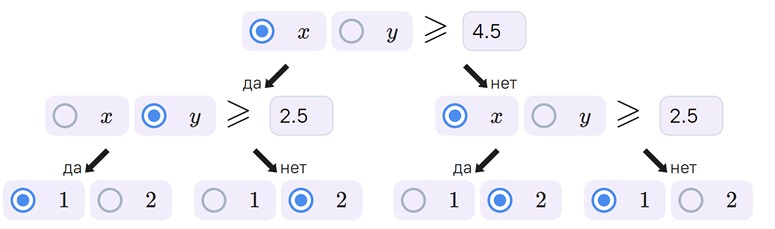
Решающее дерево глубины 2 — это полное бинарное дерево с 7 вершинами: в 4 листьях стоят предсказанные классы, в 3 внутренних вершинах — пороговые условия на одну переменную, например, 𝑦 ⩾ 2.5 (то есть проверки вида 𝑥 ⩾ 𝑡или 𝑦 ⩾ 𝑡). Пример такого решающего дерева приведён ниже. Заполните пропуски в решающем дереве глубины 2 так, чтобы доля правильно предсказанных ответов оказалась наибольшей.
Ответ:
Задание 4. Тикеты поддержки
В службе поддержки каждый тикет автоматически помечается вероятностью того, что он критический. Есть разные издержки: если пометим критическим обычный тикет, придётся зря отвлекать команду, а если не заметим критический тикет, понесём серьёзные потери. Дан файл, который вы можете скачать в форматах XLSX, ODS или CSV. В каждой строке файла записаны четыре значения:
prob — предсказанная вероятность того, что тикет критический, число из интервала [0,1];
label — истинная метка: 0 (обычный тикет) или 1 (критический);
costFP — штраф за ложное срабатывание;
costFN — штраф за пропуск критического тикета.
Для каждой строки применяется следующее правило классификации:
Для скольких строк предсказание совпадёт с истинной меткой, то есть 𝑦 = label?
Ответ: 819
Задание 5. Кросс-валидация
Однажды Саша решил обучить классификатор. К сожалению, ресурсов на сложную нейронную сеть у него не было, поэтому он решил, что классификатор будет предсказывать класс, который чаще всего встречался в обучающих данных. Если таких было несколько, он будет предсказывать класс с наименьшим номером. Саша недавно узнал о кросс-валидации и поэтому решил оценить свою модель именно с помощью неё. Всего у Саши есть 𝑛 объектов, 𝑖-й из которых имеет класс 𝑐𝑖. Для кросс-валидации Саша разделил эти данные на части по 𝑡 объектов (последняя часть при этом могла оказаться короче). Для каждой из частей классификатор обучается на данных из всех остальных частей и считает число правильных ответов модели по данным из текущей части. В итоге он суммирует число правильных ответов для всех разбиений. Таким образом, получается некоторая оценка точности модели. Помогите Саше: найдите значение точности модели, посчитанное с помощью кросс-валидации.
Ответ: 1 правильное предсказание.
Задание 6. Шаг K-Means
Современные сервисы, такие как карты или маркетплейсы, часто используют кластеризацию — разбиение множества объектов на группы по сходству. Например, можно сгруппировать магазины по районам или фотографии по похожим цветам. Один из самых простых и популярных методов кластеризации — k-means.
Этот метод ищет группы точек, расположенных близко друг к другу. Основная идея состоит в том, что каждая группа описывается своим центром (средней точкой), а обучение происходит итерационно: точки относят к ближайшим центрам, а затем центры пересчитывают как среднее значение всех точек, попавших в группу. Эта простая идея лежит в основе многих систем машинного обучения и анализа данных. В этой задаче вам предстоит реализовать один шаг обновления центров кластеров. Имеется множество точек на плоскости и несколько текущих центров. Необходимо выполнить стандартную операцию алгоритма k-means:
1. Каждая точка относится к ближайшему центру.
2. Координаты каждого центра заменяются на среднее арифметическое координат всех точек, отнесённых к нему. Если к центру не относится ни одна точка, то его положение не меняется. Если точка одинаково близка к нескольким центрам, она относится к тому, у которого первая координата меньше, а при их равенстве — вторая координата меньше. Координаты новых центров необходимо вывести в том же порядке, в котором заданы исходные центры.

