1 Ответ
1. Робот оснащён двумя отдельно управляемыми колёсами одинакового радиуса, напрямую подсоединёнными к моторам. Левым колесом управляет мотор A, правым — мотор B. На сколько градусов должна повернуться ось мотора A (при работающем с той же частотой оборотов моторе B), чтобы робот проехал прямолинейный участок трассы, указанный на схеме? Примите π ≈ 3.14.
Решение:
9 м 4 дм 2 см = 942 см
Определим угол поворота оси мотора:
942 : (2 · 12 · 3.14) · 360° = 4500°.
Ответ: 4500
2. Робот оснащён двумя отдельно управляемыми колёсами равного диаметра, напрямую подсоединёнными к моторам. Левым колесом управляет мотор A, правым — мотор B. Моторы на роботе установлены так, что если обе оси повернутся на 10°, то робот проедет вперёд прямо. Ось мотора A повернулась на 150°, и одновременно ось мотора B повернулась на –150° (ось мотора B вращается в противоположную сторону поотношению к оси мотора A). Диаметр колёс робота и ширина колеи указаны на схеме. Определите длину траектории, по которой переместился центр колеса A. Ответ выразите в сантиметрах, округлите до десятых. Примите π ≈ 3.14.
Ответ: 15.7
3. Рабочая зона манипулятора имеет форму сектора кольца. Размеры на рисунке даны в сантиметрах.
Определите площадь рабочей зоны манипулятора. Ответ выразите в квадратных дециметрах, округлите до десятых. Примите π ≈ 3.14.
Решение:
25 см = 2.5 дм
40 см = 4 дм
Площадь рабочей области манипулятора:
π∙(42-2,52)∙ 135°/360°=11,480…=11,480… ≈11,5(дм2)
Ответ: 11.5
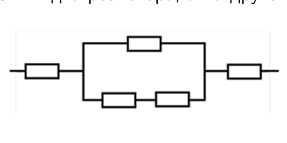
4. На макетной плате собрали участок цепи. Какая схема соответствует конфигурации данного участка цепи?
Решение:
Дорисуем на схеме проводники, расположенные внутри макетной платы и задействованные в схеме:
Теперь мы видим, что это смешанное соединение. К участку с двумя последовательно подключёнными резисторами последовательно подключён участок, содержащий две ветки параллельного соединения. На одной из них два резистора, а на другой — один. Значит, нам подходит только вариант схемы
5. Робот движется по ровной горизонтальной поверхности и наносит на неё изображение выпуклого четырёхугольника при помощи кисти, закреплённой посередине между колёс. Робот не может ехать назад.
∠A:∠B:∠C:∠D=2:3:5:6
Под суммарным углом поворота понимается сумма величин углов поворота, при этом направление поворотов робота не учитывается. Так как робот не может ехать назад, угол поворота робота равен углу, дополняющему угол многоугольника до 180°. Определите минимальный суммарный угол поворота робота при проезде по всей траектории. Место старта выберите на траектории самостоятельно. Ответ выразите в градусах. Все повороты робот должен совершать на месте.
Решение:
Обозначим Х одну часть угла, тогда углы четырехугольника будут 2Х, 3Х, 5Х и 6Х. Так как сумма углов выпуклого четырёхугольника равна 360°, составим уравнение:
2Х+3Х+5Х+6Х=360°
16Х=360°
Х=22,5
2 · 22.5=45°
3 · 22.5=67.5°
5 · 22.5=112.5°
6 · 22.5=135°
В качестве точки старта выгоднее всего выбрать вершину угла с наименьшей градусной мерой из имеющихся, в данном случае это угол 45°. Посчитаем градусную меру минимального суммарного угла поворота:
180°- 67.5° + 180° — 112.5° + 180° — 135° = 225°.
Ответ: 225
6. По правилам робототехнических соревнований «Тир» необходимо собрать на полигоне устройство, обеспечивающее одновременное горизонтальное перемещение двух мишеней с одинаковой скоростью. Так как мишени достаточно тяжёлые и должны располагаться на относительно большом расстоянии друг от друга, Таня решила сделать два отдельных механизма, каждый из которых состоит из мотора, зубчатого колеса и рейки. В распоряжении Тани есть два одинаковых мотора, по одной шестерне с 24 зубьями и
с 40 зубьями и две зубчатые рейки необходимой длины. На валу первого мотора закреплена шестерня с 24 зубьями. На валу колёс второго мотора закреплена шестерня с 40 зубьями. Обе шестерёнки могут войти в зацепление с рейками (модули зубчатых и реек одинаковые). Мотор первого механизма делает 4 оборота в секунду. Сколько оборотов в минуту должен делать мотор второго механизма для обеспечения одинаковой скорости перемещения мишеней?
Решение:
4 об/c = 240 об/мин
Для обеспечения одинаковой скорости перемещения мишеней необходимо, чтобы за одинаковое время зубчатые колеса проворачивались на одинаковое количество зубьев, то есть за минуту
240 об/мин · 24 = X об/мин · 40,
где X частота вращения мотора второго механизма
X = 240 · 24 : 40= 144 об/мин.
Ответ: 144
7. В робототехнике для определения расстояния часто используются ультразвуковые датчики. Популярным и относительно недорогим датчиком является US−015. Как видно из рисунка, у датчика 4 контакта: VCC — питание, GND — «земля», Trig — контакт триггера, Echo — контакт echo. На контакт Trig подаётся импульс высокого уровня длительностью 10 мкс, датчик формирует серию из 8 ультразвуковых импульсов частотой 40 кГц, после этого устанавливает высокий уровень на контакте Echo. При получении отражённого от объекта (препятствия, стены и пр.) ультразвукового сигнала на контакте Echo устанавливается низкий уровень. Таким образом, измерив длительность сигнала на контакте Echo, мы можем определить расстояние до объекта. Определите расстояние до объекта, если длительность сигнала Echo составляет 308 мкс. Скорость звука в воздухе при нормальных условиях примите
равной 340 м/с. Ответ выразите в сантиметрах, округлите до сотых.
Решение:
308 мкс = 308 · 10-6 с
Расстояние, пройденное сигналом:
340 м/с · 308 · 10-6с = 104 720 · 10-6 м = 0.10472 м = 10.472 см
Так как сигнал должен пройти путь до предмета и обратно, расстояние до предмета:
10.472/2 = 5.236 см
5.236 см ≈ 5.24 см
Ответ: 5.24
8. Гоша собрал колёсного робота для соревнований по перетягиванию каната. Он использовал два одинаковых двигателя с энкодерами с точностью 1 градус. При подаче равных положительных значений на моторы командой motor(left, right) робот движется вперёд по прямой. Но, зная, что у соперников более мощные двигатели, Гоша решил поставить понижающую зубчатую передачу от моторов к колёсам. У него в распоряжении оказались только две разных больших шестерни на 24 и 40 зубьев и три маленьких на 8 зубьев. Центр тяжести робота находится посередине между колёс. Чтобы установить колёса соосно, Гоша построил передачу, как показано на рисунке. Но робот вместо движения вперёд начал крутиться.
а) Гоша догадался включить моторы с одинаковыми по модулю скоростями разных знаков. Колея робота составляет 20 см. Найдите диаметр окружности, которую опишет центр робота. Ответ выразите в сантиметрах.
б) Гоша написал программу, согласно которой робот должен вращаться в течение 180 с. Сколько полных кругов сделает робот, если диаметр колёс 40 мм, а скорость вращения оси каждого мотора равна 100 rpm? Ответ округлите до целых.
в) Гоша нашёл алгоритм, который можно было бы использовать для синхронизации моторов для прямолинейного движения со средней положительной скоростью speed, подаваемой на оба мотора с разными знаками, но в нём не были указаны значения коэффициентов k1 и k2.
while(true){
e = k1 * encoderLeft + k2 * encoderRight;
left = speed + e;
right = speed – e;
motor(left, –right);
36
}
sleep(1);
Определите наименьшие по модулю целые значения этих коэффициентов. При расчёте считайте, что показания энкодеров неотрицательные.
Ответ:
а) D = 80
б) 4
в) k1 = -3, k2 = 5
