1 Ответ
База:
Задание 1. Цена за один ананас 210 руб. Какое максимальное число ананасов можно купить на 700 руб., если их цена снизится на 20%?
Ответ: 4
Задание 2. Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
ВЕЛИЧИНЫ
ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) Объём спальной комнаты
1) 908 км3
Б) Объём ящика для фруктов
2) 72 л
В) Объём лёгких взрослого человека
3) 4 л
Г) Объём воды в Ладожском озере
4) 45 м3
Ответ: 4231
Задание 3. На рисунке показано изменение температуры воздуха на протяжении трех суток.
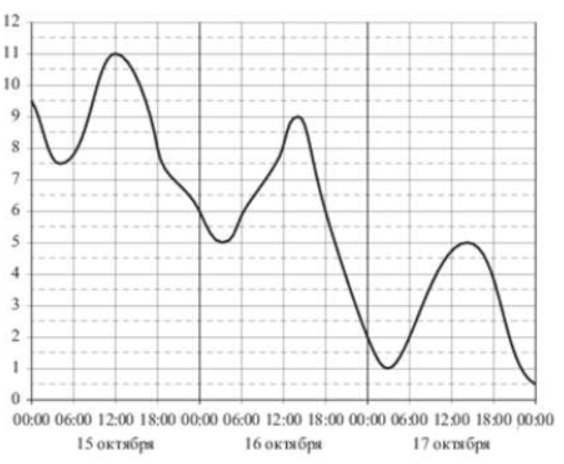
По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наибольшую температуру воздуха 17 октября. Ответ дайте в градусах Цельсия.
Ответ: 5
Задание 4. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует −7° по шкале Цельсия?
Ответ: 19,4
Задание 5. На фабрике керамической посуды 30% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до тысячных.
Ответ: 0,92
Задание 6. Семья из трёх человек планирует поехать из Москвы в Казань. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 1300 рублей. Автомобиль расходует 10 литров бензина на 100 километров пути, расстояние по шоссе равно 800 км, а цена бензина равна 48 рубля за литр. Сколько рублей придётся заплатить за наиболее дешёвую поездку на троих?
Ответ: 3840
Задание 7. На рисунках изображены графики функций вида y = kx + b.
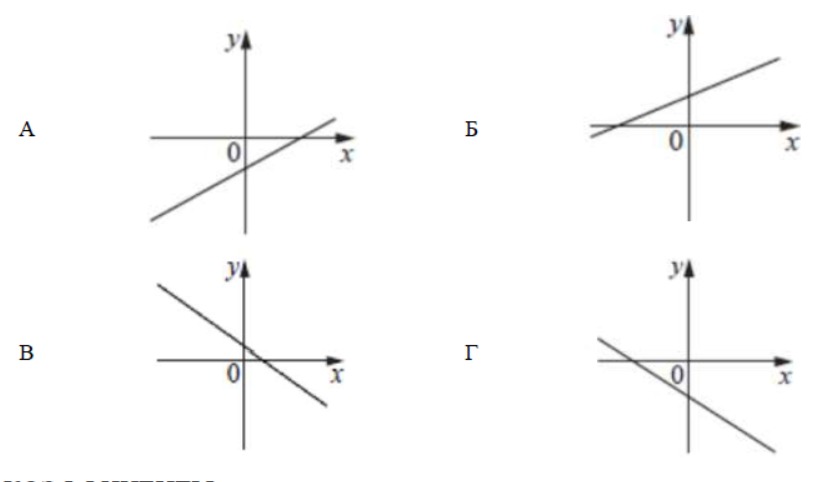
Установите соответствие между графиками функций и знаками коэффициентов k и b.
КОЭФФИЦИЕНТЫ:
1)k>0, b<0
2) k<0, b> 0
3)k<0, b<0
4) k>0, b>0
Ответ: 1423
Задание 8. В компании работают 15 переводчиков, из них 8 человек знают немецкий язык, а 12 человек — французский. Выберите утверждение, которое следует из приведённых данных.
1) в компании нет переводчика, который не знал бы ни немецкого, ни французского языка.
2) в компании найдутся хотя бы два человека, которые знают одновременно немецкий и французский языки.
3) в компании найдётся переводчик, который не знает ни немецкого, ни французского языка.
4) в компании не найдётся 8 человек, которые знают немецкий и французский языки.
В ответе запишите номер выбранного утверждения.
Решение:
Всего переводчиков: 15
Знают немецкий: 8
Знают французский: 12
Сумма знающих немецкий и французский: 8 + 12 = 20
Так как 20 больше, чем общее количество переводчиков (15), это означает, что есть люди, которые знают оба языка.
Разница 20 — 15 = 5 показывает, что как минимум 5 человек знают оба языка.
Единственное утверждение, которое точно следует из данных, — это утверждение номер 2.
Ответ: 2
Задание 9. Найдите площадь треугольника, изображенного на клетчатой бумаге с линейным размером клетки 3 см (см. рис.). Ответ дайте в сантиметрах
Ответ: 144
Задание 10. Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите общую длину забора в метрах.
Ответ: 135
Профи:
Задание 1. В прямоугольном треугольнике ABC с прямым углом С, АВ = 234, АС = 90. Найдите tgA.
Ответ: 2,4
Задание 2. Диагонали ромба ABCD равны 5 и 6. Найдите квадрат длины вектора BD+ AC.
Ответ: 61
Задание 3. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Разница объемов шара и конуса равна 3. Найдите сумму их объемов.
Ответ: 5
Задание 4. В классе 26 учащихся, среди них есть два друга. Класс случайным образом разбивают на 2 равные команды. Найдите вероятность того, что друзья окажутся в одной команде.
Ответ: 0,47
Задание 5. В кармане у Пети было 4 монеты по два рубля и 2 монеты по пять рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что обе пятирублёвые монеты лежат в одном кармане.
Ответ: 0,4
Задание 6. Найдите корень уравнения: og11(7-x)=10gu (4-x)+1.
Ответ: 3,7
Задание 7. Найдите
У(x+a)+y(а-х)-3, если y(x)=5х-2а
Ответ: -7
Задание 8. Прямая у = 5x + 2 параллельна касательной к графику функции у = x2-7x + 3. Найдите абсциссу точки касания.
Ответ:
Задание 9. После дождя уровень воды в колодце повышается. Если измерить время t падения небольших камешков в колодец, то можно рассчитать расстояние до воды по формуле h=6t2, где h – расстояние в метрах, t – время падения в секундах. До дождя время падения камешков составляло 0,5 секунд. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 секунд? Ответ выразите в сантиметрах.
Решение:
Рассчитаем расстояние до воды до дождя:
h1 = 6 * (0.5)^2 = 6 * 0.25 = 1.5 метра.
Рассчитаем время падения камешков после дождя:
t2 = 0.5 — 0.2 = 0.3 секунды.
Рассчитаем расстояние до воды после дождя:
h2 = 6 * (0.3)^2 = 6 * 0.09 = 0.54 метра.
Рассчитаем, на сколько поднялся уровень воды:
Δh = h1 — h2 = 1.5 — 0.54 = 0.96 метра.
Переведем результат в сантиметры:
96 метра = 96 сантиметров
Ответ: Уровень воды должен подняться на 96 сантиметров.
