1 Ответ
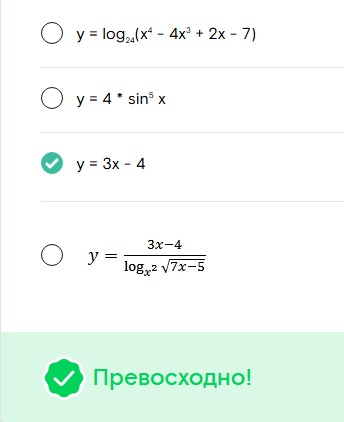
1. Какая из приведенных функций – простая? Выберите верный вариант ответа.
2. Функция непрерывна и определена при всех действительных числах. До некоторой точки она убывала, а потом стала возрастать. Сколько раз производная этой функции принимала значение 0?
Решение:
Если функция непрерывна и определена при всех действительных числах, и до некоторой точки она убывала, а потом стала возрастать, то это означает, что у нее есть точка минимума.
В точке минимума производная функции равна 0. Поскольку до этой точки функция убывала, а после — возрастала, то производная меняет свой знак с отрицательного на положительный.
Таким образом производная этой функции принимает значение 0 ровно один раз в точке минимума.
Ответ: 1
3. Найдите значение производной (x^a)’, если a = 3, x = 4. Ответ запишите в виде числа.
Решение:
Используем правило дифференцирования степенной функции: (x^a)’ = a * x^(a-1)
Подставляем a = 3 и x = 4:
(x^3)’ = 3 * x^(3-1) = 3 * x^2
Теперь подставляем x = 4:
3 * 4^2 = 3 * 16 = 48
Ответ: 48
