1 Ответ
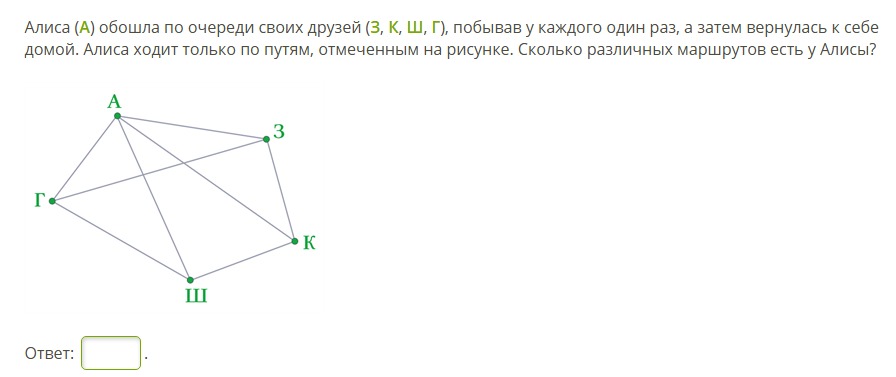
1. Алиса (А) обошла по очереди своих друзей (3, К, Ш, Г), побывав у каждого один раз, а затем вернулась к себе домой. Алиса ходит только по путям, отмеченным на рисунке. Сколько различных маршрутов есть у Алисы?
Ответ: 8
2. Обходя ограду королевского дворца с наружной стороны, рыцарь Ланселот преодолевает на 80 метров больше, чем при обходе этой ограды с внутренней стороны (движение строго по периметру). Чему равна толщина ограды? (Толщину ограды считаем одинаковой всюду, движение строго по периметру, т.е. пренебрегаем расстоянием между оградой и рыцарем.)
Ответ: 10м
3. Дима придумал такую игру: сначала он загадал цифру от 1 до 9, затем умножил её на 8 и взял последнюю цифру результата. На этом он не остановился и разделил полученную цифру на 2, к результату прибавил 4, затем умножил всё на 5 и вычел 3. Наконец, он взял только последнюю цифру результата. Найди и запиши сумму максимального и минимального результатов, которые могут быть получены после применения всех операций.
Ответ: 9
4. У гнома Алвина есть волшебный сундук. Если положить в него № монет и закрыть на минуту, то количество монет увеличится на сумму цифр числа N. Какое максимальное число монет Алвин сможет получить за 20 минут, если изначально у него есть 1 монета? (Указанное время отражает действие сундука. Временем, уходящим на перекладывание монет, можно пренебречь.)
Ответ: 267 монет
5. Имя Денис в некоторой системе составляет 14 единиц, Виталина — 28, Кай и Кир — по 7, а Арсений — 21. Сколько единиц составляет имя Валентина в той же самой системе?
Решение:
В данной системе каждая буква имени соответствует определенному числовому значению. Чтобы определить это значение, можно проанализировать предоставленные данные:
Денис (14): Д + е + н + и + с = 14
Виталина (28): В + и + т + а + л + и + н + а = 28
Ответ: 28
6. Карлсон съедает 3 литра сгущёнки за 20 минут, а Винни-Пух — 4 литра сгущёнки за 40 минут. Сколько минут потребуется Карлсону и Винни-Пуху, чтобы съесть 1 литр сгущёнки вместе?
Ответ: 4 Мин.
Решение:
Находим скорость поедания сгущёнки для каждого:
Карлсон: 3 литра / 20 минут = 0.15 литра в минуту
Винни-Пух: 4 литра / 40 минут = 0.1 литра в минуту
Находим их общую скорость поедания:
0.15 литра/минуту + 0.1 литра/минуту = 0.25 литра в минуту
Рассчитываем время, чтобы съесть 1 литр вместе:
1 литр / 0.25 литра/минуту = 4 минуты
Ответ: 4 Мин.
7. Кузнечик стоит на отметке п см на линейке. Он движется по определённым правилам:
Сначала он прыгает вперёд на 3 см, пока не окажется на числе, которое делится на 5 (если п изначально
делится на 5, то ничего не происходит);
Как только такое число достигнуто, он перескакивает на число, в 5 раз меньшее;
После этого он снова начинает прыгать по тем же правилам.
Выбери первые пять значений п, начиная с которых в результате таких действий можно добраться до отметки 1 см.
Ответ: 1, 2, 4, 5, 7
8. Пусть все клетки доски 100 х 100 покрашены в красный и зелёный цвета. Клетка называется гармоничной, если у неё равное количество красных и зелёных соседей. Каково максимально возможное количество гармоничных клеток? (Клетки считаются соседями, если у них имеется общая сторона.
Ответ: 9608
9. Назовём натуральное число лестничным, если его цифры строго возрастают слева направо (например, 12 или 479). Какое наименьшее количество лестничных чисел надо сложить, чтобы получить 2235?
01
02
03
04 +
05
06
07
08
09
Использованные числа: 1689, 489, 56, 1.
Проверка: 1689 + 489 + 56 + 1 = 2235.
10. На клетчатом листе нарисованы два прямоугольника точно по линиям клеток. У первого прямоугольника
вертикальная сторона длиннее горизонтальной, а у второго — наоборот. Какой может быть максимально
возможная площадь их пересечения, если первый прямоугольник состоит из 225 клеток, а второй — из 224?
(Наложения происходят только по вертикали и горизонтали, то есть пересечение тоже является
прямоугольником, составленным из клеток.)
Решение:
Выберем такую комбинацию множителей, чтобы их произведение было строго меньше 15, но чтобы это было наибольшее возможное число.
Для числа 225 — 3 3 = 9.
Для числа 224 — 2 — 7 = 14.
Получается, площадь пересечения не превосходит 9 — 14 = 126 клеток. Это реализуется при размерах прямоугольников 9 * 25 и 14 * 16.
Ответ: 126
