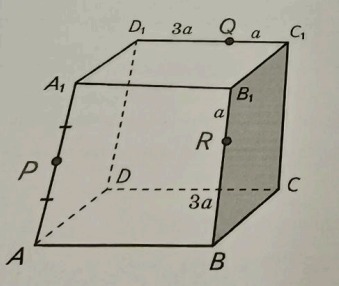
На ребрах куба ABCDA1B1C1D2 отметили точки P, Q и R. Постройте сечение куба плоскостью (PQR). В каком отношении эта плоскость делит ребро B1C1?
Опишите алгоритм соответствующего построения. Запишите в ответе искомое соотношение, не приводя доказательства.
Дано:
Алгоритм построения:
Куб ABCDA: B1 C D1, Р — середина AA1, R BB1, Q E C Di, причем BR : B1R = D1Q: C1Q = 3 : 1.
Построить: Сечение куба плоскостью (PQR).
1 Ответ
Решение:
1) В условии дано:
Куб ABCDA₁B₁C₁D₁
P — середина AA₁
R ∈ BB₁
Q ∈ C₁D₁
BR : B₁R = D₁Q : C₁Q = 3 : 1
2) Нам нужно найти, в каком отношении плоскость (PQR) делит ребро B₁C₁.
3) Алгоритм решения:
1. На ребре BB₁ точка R делит его в отношении 3:1 (считая от точки B)
2. На ребре C₁D₁ точка Q делит его в отношении 3:1 (считая от D₁)
3. Точка P — середина AA₁, значит делит ребро в отношении 1:1
4) Применяя теорему о пересечении плоскости с параллельными прямыми (если плоскость пересекает одну из параллельных прямых, то она пересекает и другую, причем отношение отрезков сохраняется), получаем:
Плоскость (PQR) пересекает ребро B₁C₁ в точке, которая делит это ребро в отношении 3:1 (считая от B₁).
Ответ: B₁K : KC₁ = 3 : 1, где K — точка пересечения плоскости (PQR) с ребром B₁C₁.
