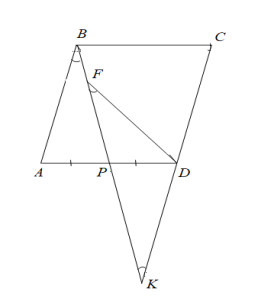
В параллелограмме АВСD точка P середина AD. Найдите длину отрезка FD, если стороны параллелограмма AB = 5, BC = 6?

Решение:
Продлим прямую BP за точку P до её пересечения с прямой СD. Получим точку K.
Рассмотрим треугольники ABP и DKP.
Так как AP = PD, ∠APB = ∠DPK и ∠BAP = ∠PDK, то ∆ABP = ∆DKP и KD = AB. ∆FDK – равнобедренный, так как ∠PFD = ∠DKP, следовательно, FD = KD = AB = 5.
Ответ: 5