1 Ответ
Задание 1.
Почтовая марка
Команда дизайнеров работает над созданием макета почтовой марки с использованием новаторской квадратной перфорации. Подготовленное художником изображение имеет размеры w миллиметров в ширину и h миллиметров в высоту (для удобства дальнейшей работы эти величины выражаются нечётными натуральными числами). Рисунок печатается в типографии с белыми полями шириной 2 миллиметра со всех сторон, после чего осуществляется перфорация, как показано на рисунке.
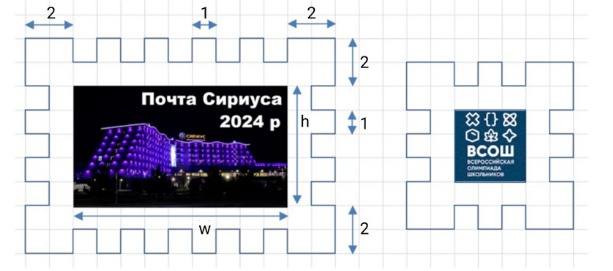
По данным ширине w и высоте h изображения определите периметр получившейся почтовой марки.
Ответом на эту задачу является некоторое выражение, которое может содержать целые числа, переменные w и h (обозначаются английскими буквами), операции сложения (обозначаются +), вычитания (обозначаются −), умножения (обозначаются *) и круглые скобки. Запись вида 2h для обозначения произведения числа 2 и переменной h некорректна, нужно писать 2 * h.
Ваше выражение должно давать правильный ответ для любых нечётных натуральных значений w и h. Например, для приведённых на первом рисунке w=9 и h=5 значение выражения должно быть равно 76, а для приведённых на втором рисунке w=h=3 значение выражения должно быть равно 4.
Пример правильной формы записи ответа:
w𝑤 * h−2 * (h−1)
Ответ:
2. Задание 2.
Диалог нейросетей
Две нейросети ведут между собой диалог, по очереди записывая слова. Слова добавляются в конец уже существующей строки без дополнительных пробелов. Каждая из программ знает только четыре слова: «push», «pop», «in» и «offtop», то есть в итоге получится строка, составленная только из этих слов, без пробелов. Диалог будет считаться успешным, если выполнены следующие условия:
1. Первое и последнее слово этого диалога «push».
2. В диалоге встречаются хотя бы по одному разу все четыре слова «push», «pop», «in» и «offtop».
3. В диалоге нигде не встречаются следующие подстроки (то есть подряд идущие символы): «hinp», «pinp», «popp», «npopo», «hpopi», «npu».
Например, диалог «pushpopinofftoppush» не будет успешным, так как в нём встречается подстрока «hpopi». Диалог «pushinofftoppush» не будет успешным, потому что в нём не использовано слово «pop». А диалог «pushinofftoppop» не будет успешным, потому что он не заканчивается словом «push».
Требуется найти успешный диалог, содержащий как можно меньше букв.
Решение:
Правильный ответ будет «pushinofftoppoppush». Эта строка удовлетворяет всем требуемым условиям: она начинается и заканчивается на «push», содержит все четыре слова хотя бы по одному разу и не содержит недопустимые подстроки.
3. Задание 3.
Робот‑пылесос
Современные роботы‑пылесосы очень умные. Например, они способны в своей памяти строить карту помещения, разбивать помещение на сектора и даже прогнозировать загрязнения каждого сектора. Сектора, закрашенные в чёрный цвет, недоступны для уборки. Там, вероятно, стоит диван, кресло или какое‑то другое препятствие. Число на секторе —— это прогнозируемое количество пыли. У робота‑пылесоса, который отмечен на карте помещения рисунком, заканчивается заряд батареи, и пылесос может выполнить только X перемещений в соседний сектор. По какому маршруту лучше пройти роботу, чтобы собрать как можно больше пыли?

Робот‑пылесос может передвигаться строго по свободным секторам (не покрашенным в чёрный цвет) и не может выезжать за пределы помещения. Если пылесос сталкивается с препятствием или стеной комнаты, то он останавливается.
Маршрут пылесоса необходимо записать в виде строки из символов «U», «D», «L», «R», где «U» обозначает перемещение на один сектор вверх, «D» —— перемещение вниз, «L» —— перемещение влево, «R» —— перемещение вправо.
Например, при движении по маршруту «URR» робот‑пылесос соберёт 5 единиц пыли, а при исполнении маршрута «RRU» соберёт 3 единицы пыли, затем столкнётся с препятствием и остановится.
Запишите маршрут движения робота‑пылесоса, при котором он сможет собрать наибольшее количество пыли при заданных X. Ответы записывайте в виде последовательностей символов «U», «D», «L», «R» без пробелов и иных разделителей.
4. Задание 4.
День борьбы
23 мая отмечается Международный день спортивной борьбы.
Отрывной календарь
Поскольку соревнования по спортивному программированию часто проходит в остановке острой, напряжённой и упорной борьбы, правительство Берляндии поручило национальной федерации этого вида спорта организовывать и проводить все олимпиады по информатике в стране.
По мнению главы федерации, важнейшей характеристикой спортсмена (а теперь и программиста) является его вес. Поэтому атлетов распределяют на весовые категории, соперники в которых сравнительно равны по физическим возможностям.
Для первой олимпиады, проводимой под эгидой федерации, было принято решение разделить всех 1000 участников всего лишь на три весовые категории (лёгкую, среднюю и тяжёлую).
На церемонии открытия олимпиады все программисты одной весовой категории выходят на специальный помост для приветствия и фотографирования. Важнейшей характеристикой такого помоста является прочность —— он должен выдержать вес всех поднявшихся на него атлетов. Помогите организаторам определить границы весовых категорий таким образом, чтобы наибольший суммарный вес борцов из одной весовой категории был наименьшим.
Найдите такое подходящее разбиение участников по весовым категориям, чтобы суммы весов первых A спортсменов (с наименьшим весом), следующих B спортсменов и последних C𝐶 спортсменов (с наибольшим весом) из предложенного списка отличались как можно меньше. При этом спортсмены с одинаковым весом должны находиться в одной весовой категории.
В качестве ответа запишите три числа A, B, C, дающие в сумме 1000. Баллы будут начисляться только за такие ответы, в которых спортсмены с одинаковым весом целиком попадают в одну весовую категорию. При этом чем меньше будет наибольший суммарный вес участников одной весовой категории, тем больше баллов получит решение.
Замечание
Пример: в соревновании принимают участие 10 спортсменов и их веса равны 10, 20, 30, 30, 40, 40, 50, 50, 60, 100.
Назначим шесть первых программистов в лёгкую весовую категорию (их суммарный вес 170), двух следующих —— в среднюю (100), двух последних —— в тяжёлую (160). Тогда помост должен выдерживать вес 170. Такой же результат даст ещё одно разбиение: шесть первых спортсменов назначить в лёгкую весовую категорию (170), трёх следующих —— в среднюю (160), последнего —— в тяжёлую (100). Если пять первых программистов назначить в лёгкую весовую категорию (130), трёх следующих —— в среднюю (140), двух последних —— в тяжёлую (160), то, на первый взгляд, можно достигнуть ещё более оптимальной прочности помоста —— 160. Но тогда пятый и шестой участники (имеющие равный вес) окажутся в разных весовых категориях, что является нарушением спортивного принципа. Ответом в этом примере будут числа 6, 2, 2 или 6, 3, 1.
5. Обои и дипломы
Родители Андрея решили поклеить на одну из стен в его комнате новые обои. Высота стены —— n сантиметров, а ширина —— m сантиметров. К сожалению, обои, выбранные родителями, Андрею не понравились, и он решил их чем‑нибудь закрыть. Так как он участвовал в большом количестве олимпиад, у него накопилось много дипломов. Все дипломы у Андрея одинаковые —— это прямоугольники высотой a𝑎 сантиметров и шириной b сантиметров. Помогите Андрею узнать, сколько квадратных сантиметров обоев он сможет завесить дипломами, если не будет их разрезать и переворачивать. Все дипломы должны целиком размещаться внутри стены и не накладываться друг на друга.
Формат входных данных
В первой строке входных данных находится целое число n𝑛 (1≤n≤2⋅109) —— высота стены.
Во второй строке находится целое число m𝑚 (1≤m≤2⋅10^9) —— ширина стены.
В третьей строке находится целое число a𝑎 (1≤a≤2⋅10^9) —— высота диплома.
В четвёртой строке находится целое число b𝑏 (1≤b≤2⋅10^9) —— ширина диплома.
Выведите одно целое число —— площадь части стены, которая будет закрыта дипломами, если их не поворачивать, не обрезать и не накладывать друг на друга.
6. Задание 6.
Светофор
Студент Павел недавно приобрёл себе подержанный автомобиль и теперь ездит на нём в университет. На его пути в вуз имеется один загруженный перекрёсток, проезд через который регулируется светофором. Сделав ряд поездок, Павел обнаружил интересную закономерность: пока на светофоре горит зелёный свет, через перекрёсток успевает проехать не менее a, но не более b машин.
Сверху над перекрёстком установлена уличная видеокамера. Павел может подключиться к ней со своего смартфона и сосчитать количество машин n𝑛, которые стоят перед светофором впереди него (свою машину он тоже считает).
Назовём тактом светофора включение на нём зелёного сигнала. Напишите программу, определяющую минимальный и максимальный номер такта, на котором Павел проедет перекрёсток.
Задание 7.
Робот
На бесконечной в обе стороны клетчатой полоске в клетке с нулевой координатой стоит робот.

Робот делает 1 шаг вправо, затем 2 шага влево, 3 шага вправо, 4 шага влево и так далее. Сделав суммарно N шагов, робот останавливается. Определите координату клетки, в которой окажется робот после остановки.
Ответы появятся по мере их решения!
