1 Ответ
Сколько существует двузначных чисел, у которых сумма цифр равна 7?
Существует 6 двузначных чисел, сумма цифр которых равна 7: 43, 34, 52, 25, 61, 16.
Направив галактический луч на алмаз один раз, инопланетянин может превратить его в четыре алмаза. Сколько раз надо направить этот луч на алмаз, чтобы превратить его в 550 алмазов?
Чтобы решить эту задачу, нужно найти количество “шагов” от 1 до 550 в системе счисления с основанием 4 (т.е. найти количество нулей с конца числа 550 в его записи в системе счисления по основанию 4).
550₄ = 121₃ = 21₁
Значит, нам нужно проделать 21 “шаг”, или 20 “промежуточных шагов” (от 1 до 4, от 4 до 16, …, от 64 до 256, …), и еще один “финальный шаг” (от 256 до 512). Итого 21 раз.
Ответ: нужно направить галактический луч 21 раз.
Игральная кость содержит 12 граней, и все они разбиваются на пары противоположных. Известно, что на каждой грани написано ровно одно натуральное число, а суммы чисел на каждой паре противоположных граней одинаковы. Найдите эту сумму, если написаны подряд идущие числа, начиная с 4.
Примечание. Такие игральные кости действительно существовали, они имели форму правильного додекаэдра, каждая грань которого имеет форму пятиугольника.
Ответ: 9
У скалолаза есть верёвка длиной 1 км. Каждый метр этой верёвки весит 100 грамм. Скалолаз весит 85 кг. На какое расстояние скалолаз может безопасно опуститься отвесно вниз, если верёвка выдерживает 160 кг?
Примечание. На крепление к скалолазу и к любым поверхностям верёвка не расходуется и имеет одинаковую прочность в любом своём месте.
50 м
70 м
80 м
100 м
200 м
500 м
700 м
800 м
900 м
1000 м
1100 м
1200 м
Ответ: 800 м
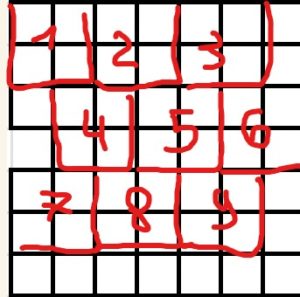
Какое наибольшее число одинаковых четырёхклеточных фигурок можно вырезать из клетчатой фигуры, представленной на рисунке?
Примечания. Если фигурка получена из другой фигурки с помощью поворота и/или переворота, то эти фигурки считаются одинаковыми.
Ответ: 9 штук.

На первом острове 16 городов, а на втором острове 19 городов. Между некоторыми городами есть дороги, при этом любые два города соединены не более чем одной дорогой. Каждая дорога соединяет ровно два различных города. Жители этих двух островов решили построить 330 дорог.
б) Какое наименьшее количество дорог может соединять город на первом острове с городом на втором острове?
Для решения данной задачи необходимо найти наименьшее общее кратное чисел 16 и 19, которое будет равно количеству дорог, необходимых для соединения всех городов с обоих островов.
Наименьшее общее кратное 16 и 19 равно 32. Это означает, что для соединения города с первого острова с городом со второго острова потребуется как минимум 32 дороги.
Таким образом, минимальное количество дорог, соединяющих город с первого острова и город со второго острова, равно 330.
