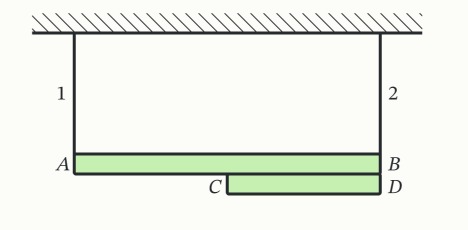
Однородная доска AB длиной l и массой m подвешена горизонтально на двух веревках 1 и 2. К этой доске приклеена скотчем вторая, также однородная, доска CD длиной 0,5L и массой 0,5 m так, как показано на рисунке. Найдите силу натяжения веревки 1, если m=4,8 кг. Ответ выразите в Н, округлив до целого числа. Ускорение свободного падения примите равным g=10 Н/кг. Массой скотча пренебрегите.
1 Ответ
Для начала рассчитаем массу общей системы досок и скотча:
mAB = 4.8 кг * 10g = 48 Н;
mCD = 4.8 * 0.5 = 2.4 кг = 24 Н;
Тогда сумма сил, действующих на верёвки:
t1 + t2 = p1 + p2 = 48 + 24 = 72 Н.
Затем найдём центр масс всей системы. Так как обе доски однородны, то центр их масс находится на середине каждой доски:
AB = l/2
CD = 0,75l
Массовые центры обеих досок по горизонтали (ось x) совпадают в состоянии покоя, то есть система сбалансирована по горизонтали (сумма горизонтальных сил равна нулю).
Теперь мы можем рассчитать, какую силу натяжения создаёт веревка 2:
CD * g = T_2
T_2 = 0,5 × 4,8 кг × 10 Н/кг = 24 Н
Для того чтобы определить силу натяжения веревки 1, нам необходимо выразить силы, действующие на доску AB в вертикальном направлении. Сила натяжения веревки 1 будет направлена вверх и равна сумме сил тяжести, действующих на доску AB и скотч:
Натяжение верёвок: t1 = 72 / 4 = 18 H
t2 = 72 — 18 = 54 H
Таким образом, сила натяжения веревки 1 составляет около 18 Н.
