В прямоугольном треугольнике катеты равны 3 и 4. Найдите расстояние между центрами вписанной и описанной окружностей. В ответ запишите квадрат этого расстояния.
1 Ответ
Решение.
По теореме Пифагора гипотенуза равна 5, площадь треугольника равна S = 1/2 * 3 * 4 = 6.
Полупериметр P 3 + 4+ 5/2 = 6 тогда радиус вписанной окружности r = s/p = 1. Пусть О1 – центр вписанной окружности, О1Р и О1К – радиусы вписанной окружности, проведенные соответственно к катету и гипотенузе в точках касания окружности, катеты ВС=4, АС=3 по условию. Имеем ВР=ВС–r=4–1=3. По свойству
касательных, проведенных из одной точки к окружности, ВК=ВР=3. Центр описанной окружности О2 вокруг прямоугольного треугольника лежит на середине гипотенузы и ВО2=2,5.
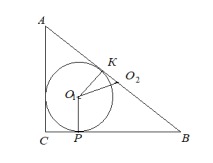
В прямоугольном треугольнике КО1О2 имеем КО2=3–2,5=0,5, КО1=r=1, О1О2 – искомое расстояние. По теореме Пифагора 0102^ = 1 + 0.25 = 1,25
Ответ: 1,25.
