Дан квадрат со стороной a. Каждую его сторону разделили на n≥2 равных частей. Для каждой вершины квадрата взяли ближайшую к ней точку разделения в порядке обхода по часовой стрелке. Выбранные точки соединили между собой так, что получился четырёхугольник, вершины которого лежат на сторонах исходного квадрата. Найдите площадь образовавшейся фигуры. На рисунке приведён пример, когда n=4.
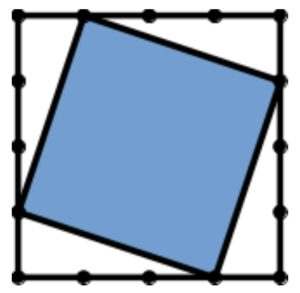
Ответом на эту задачу является некоторое выражение, которое может содержать целые числа, переменные a и n (обозначаются соответствующими английскими буквами), операции сложения (обозначаются +), вычитания (обозначаются -), умножения (обозначаются *), деления (обозначаются /) и круглые скобки. Запись вида 2a для обозначения произведения числа 2 и переменной a некорректна, нужно писать 2 * a. Для возведения значения в квадрат нужно использовать умножение, например, выражение a2 нужно записать как a * a.
Ваше выражение должно давать правильный ответ для любых значений a и n (n≥2).
Пример правильной формы записи ответа:
a * (2 * n — a / 2)
1 Ответ
Ответ:
a^2 — 2((n -1/n^2) * a^2)
